课前学习任务

考虑 ，这是个二次曲线方程. 利用 WolframAlpha 描绘其图形如下：

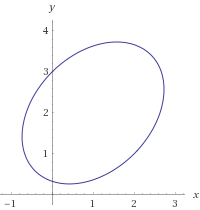
从图形推测这是一个椭圆，但它的中心不在原点，且长短轴未与坐标轴平行.

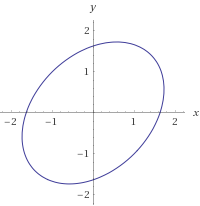
【利用平移变换可将其中心移到原点】

【利用旋转变换可使其长轴与 x 轴平行】

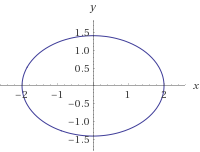
小结：大多数二次曲线方程可通过平移和旋转变换化为  的简洁形式；对空间中的二次曲面方程也有类似结果.  我们从中看到，可以利用平移变换消去方程中的一次项，从而问题的关键在于二次项，这引出了二次型的概念.

定义：数域  上的  元二次齐次多项式  称为  上的  元二次型，简称二次型.

二次齐次多项式  的一般形式为 .

课堂学习资料

课后学习任务

使用矩阵语言，n 维空间中的一般二次超曲面方程可以简洁地写成 ，其中 ，A 为 n 阶对称矩阵，，c 是一个数.

经平移变换 原方程变为

化简后得

假设 A 可逆，只需令  满足 ，则变换后的方程不含一次项.

例：考虑 3 维空间中的二次曲面方程  试解决以下问题.