著名的斐波那契数列（Fibonacci Sequence）是指满足递推关系  的一种神奇数列. 自然界许多事物的数量分布规律都遵循它. 而且非常出人意料，该数列的通项公式竟然离不开“黄金分割”这一无理数，需知斐波那契数列的每一项可都是整数！那该怎样推出斐波那契数列的通项公式呢？

【中学技巧】 作“变量替换” ，其中  是待定参数，从而

于是 . 为便于求解，当然是令 ，即 . 不妨取 ，并令 ，则 . 从而 

为方便计，令 ，则

不断迭代下去，可得

特别是当初始值  时，我们有通项 . 它产生的数列前几项为 0, 1, 1, 2, 3, 5, 8, 13, 21.

【矩阵方法】 我们知道矩阵乘法可以表达“线性替换”，因此以上技巧启发我们，或许可用矩阵的语言来表达，以致于能利用矩阵理论解决问题. 现在反观“变量替换”  及递推关系 ，它们都是关于数列相邻两项的线性表达式，故应将相邻两项视为整体，组成一个列向量 . 这样递推关系和“变量替换”就都变成了很紧凑的矩阵形式

注意前面“变量替换”中的  有两种取值，说明我们还可以作 . 即令 ，则

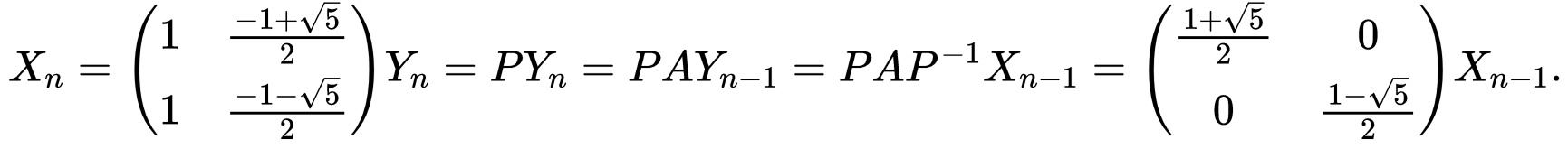
这样  的通项就很容易求出了，从而也就求出了  的通项，稍加总结如下.

如果一个数列的递推关系能够写成矩阵形式 ，则求数列的通项等价于计算矩阵的幂 ，这是因为

.

所以如果 A 是适当的上（下）三角矩阵，我们已经会利用交换矩阵的二项式定理直接计算它的幂；否则得想办法找个可逆矩阵 P 使得  为上三角阵，从而

可被直接算出，于是也能得到 . 至于这样的 P 怎么找，目前的办法是待定元素通过解方程得出，等到下学期会学到更好的办法.

课堂学习资料

课后学习资料

1. 复旦大学2015--2016学年第一学期（15级）高等代数I期末考试第七大题解答

2. 现代生活中的数学：以低秩矩阵为基础的推荐算法