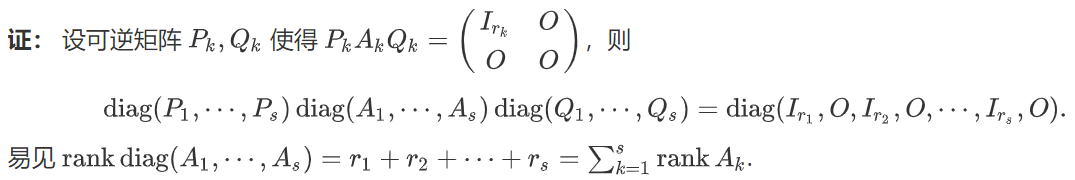【问题提出】

我们都知道，方程组当中的方程相当于是对未知元取值的约束. 通常方程越多，意味着约束越多，解的数量就越少. 但我们不能只看表面上方程的个数. 举个最极端的例子，把一个方程写一百遍，得到一个含有 100 个方程的方程组，显然这个方程组“本质上”只含一个方程. 这就提出了一个很自然的问题，就是怎样用数学语言精确地描述方程组“本质上”含几个方程. 我们需要对这个感觉到的量建立合适的数学模型.

【问题简化】

一般的方程组很难统一刻画，也过于复杂. 结合我们的背景，不妨先聚焦于齐次线性方程组. 因此把原始问题化简，并更加明确地重述出来. 所以现在的问题是，对于任意的齐次线性方程组，如何用数学语言精确地衡量其“本质上”所含方程个数？

【问题分析】

从 100 个重复方程的极端例子可以看到，之所以表面上的方程个数无法反映本质数量，是因为这些方程之间存在相互联系——只要有了其中一个，则其余 99 个就是冗余的. 为了对齐次线性方程组当中方程之间的联系有更清楚的认识，不妨考察一下较有代表性的实例.

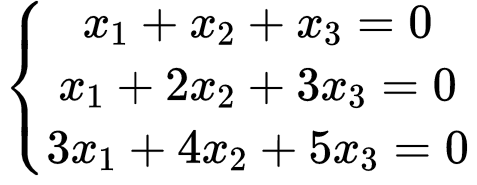
以上方程组“本质上”含几个方程？我们先用系数矩阵来表示这个方程组，即

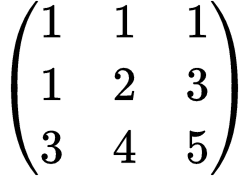
仔细观察可以发现，系数矩阵的行之间存在关系，. 这意味着，只要留下前两个方程，则第三个方程是冗余的. 换个角度，这也意味着可以利用初等行变换把第三行全变成零，即 .

另一方面，在留下的前两个方程中，则缺一不可，因为它们是“相互独立”的. 为了看得更清楚，我们还用初等行变换对它们进行等价地转化. 作 ，则第二个方程变成了 ，它和第一个方程还是“相互独立”的. 据此我们可以认为，原方程组“本质上”有两个方程.

上面的分析过程概括一下，初等行变换能够消去冗余的方程，留下“相互独立”的方程，它们的数量就是齐次线性方程组本质上含有的约束条数. 至此我们已经抓住了问题的关键线索，但如果能更深入地分析，将有助于建立更简洁优雅的数学模型. 所以我们再来分析一下初等列变换对“本质方程数”的影响.

我们知道初等列变换代表换元，而直观上，换元似乎不会改变方程之间的关系. 通过实例也能印证这一点，比如还是上面的方程组，我们对其系数矩阵作个列变换 ，于是它变成了

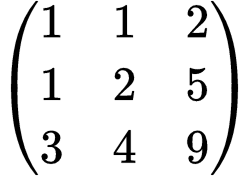
但它的行之间依然满足 .

【模型假设】

对齐次线性方程组的系数矩阵作初等变换，得到新的线性方程组，这两个方程组“本质上”所含的方程个数是相同的.

【模型建立】

任意齐次线性方程组可由它的系数矩阵表示，利用初等变换可将系数矩阵化成标准形

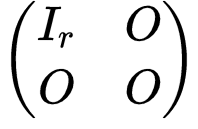
于是我们认为原方程组含有 r 条相互独立的约束，并称这个约束量 r 为原方程组或其系数矩阵的秩（rank）.

1. 矩阵的秩：基础知识及算法 （注意：该视频中的初等变换记号与我们有所不同，但不影响理解）

2. 矩阵的相抵关系 （注意：该书中全体矩阵所成集合的记号与我们有所不同，这个并不影响理解）

定理：初等变换不改变矩阵的秩.

推论 1：.

推论 2：.