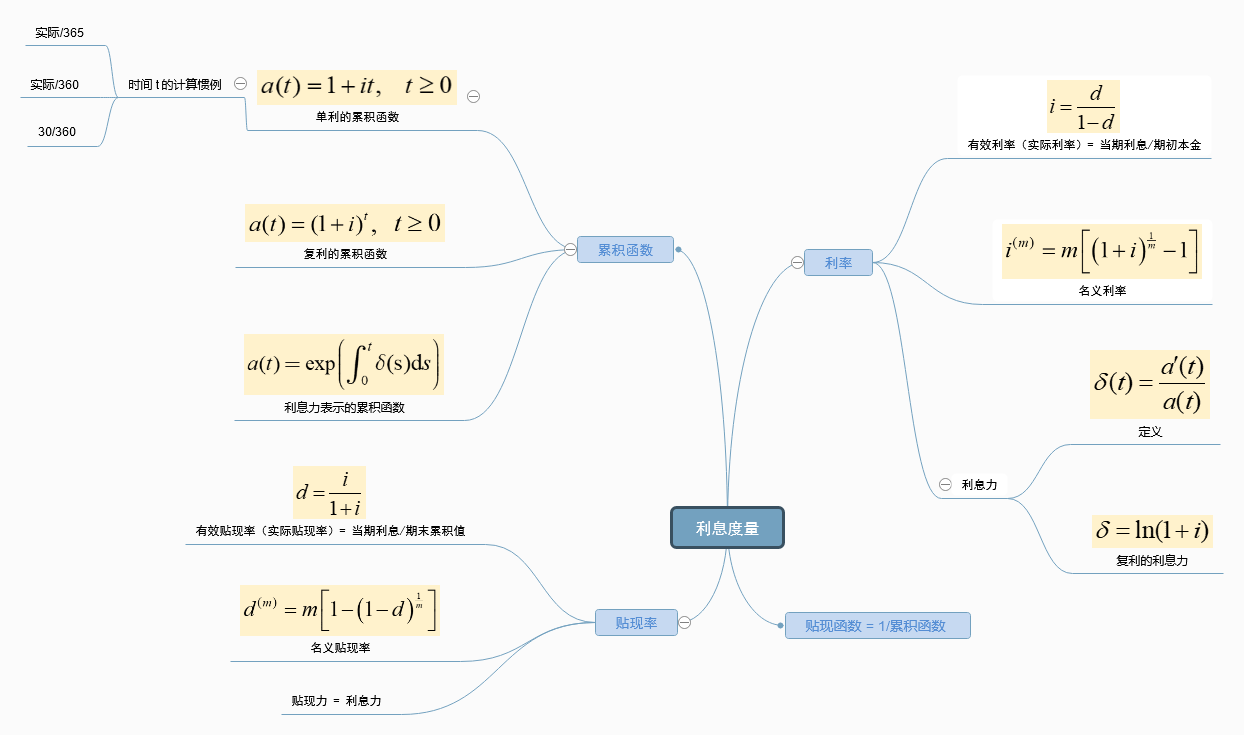
实验项目 利率的转化和日期时间差的计算
一、实验目的：
1.使用excel进行利率问题的转化计算；
2.两个日期之间时间差的计算规则；
3.在不同计息规则下利息金额的计算。
二、实验任务：
1.计算实际利率（EFFECT）；
2.计算名义利率（NOMINAL）；
3.分别利用“实际/365”“实际/360”“30/360”规则计算投资时期；
4.在以上三种规则下利息金额的计算。
三三、实验内容：请根据要求分别应用函数命令进行以下问题的求解。
1 1.每年复利4次的年名义利率为5%，计算年实际利率。
2.年实际利率为5%，计算每年复利12次的年名义利率。
3.“实际/365”规则（actual/ actual）：投资天数按两个日期之间的实际天数计算，每年按365天计算。
“实际/360 ”规则：投资天数按两个日期之间的实际天数计算，每年按360天计算。称为银行家规则 ( banker’s rule )。
“ 30/360 ”规则：每月按30天计算, 每年按360天计算。
4.投资者在2019年6月14日存入基金10000元，2020年2月7日取出，基金按单利计息，年利率为8%，分别根据下列规则计算投资者可以获得的利息金额：
（1）“实际/365”规则
（2）“实际/360” 规则
（3）“30/360” 规则
一.选择题
1. 如果年名义贴现率为6%，每四年贴现一次， 计算100万元在两年末的累积值。
A.大于100，小于110
B.大于120
C.等于120
D.小于120
2.已知时刻t的利息力为1/(t+2)，当前时刻的1单位投资在前n年赚取的利息总额为8。求n。
A.大于15，小于18
B.大于12，小于15
C.大于18
D.小于15
3.投资者在当前时刻投资100万元。假设在前两年以每个季度贴现一次的名义贴现率d计息；从t = 2 开始，按照利息力1/(1+t) 计息。在t = 5时，投资者的累积值为260万元。求d。
A.小于10%
B.小于13%
C.大于14%
D.小于12%
二.判断题
1.在给定年名义贴现率的条件下，每年贴现的次数越多，对应的年有效贴现率越大。（ ）
2. 给定了利息力，就可以写出累积函数。（ ）
3.期限为20天的理财产品的年化收益率（年名义利率）为5%，意味着其年有效收益率（年有效利率）大于5%。（ ）
三、计算题
1.每年复利4次的年名义利率为5%，计算年实际利率。
2.年实际利率为5%，计算每年复利12次的年名义利率。
3.在当前时刻将100万投入一个基金。该基金在前两年以每个季度贴现一次的名义贴现率d支付利息；从t=2开始，按照利息力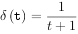
支付利息。在t=5时，投资者在该基金的累积值为260.求d的值。
4.投资者对某个基金初始投入为20万元，第10年末又投入30万元。如果此基金在前8年按每个季度末贴现一次的年名义贴现率10%计息，8年后按每半年复利一次的年名义利率6%计息.在第20年末，投资者在基金中的累积值为多少万元?
