We conclude our study of functions and modules by considering a case study of developing a program to solve an interesting scientific problem. as Monte Carlo simulation to study a natural model known as percolation.

Percolation.

We model the system as an n-by-n grid of sites. Each site is either blocked or open; open sites are initially empty. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. If there is a full site in the bottom row, then we say that the system percolates. (渗透)

 

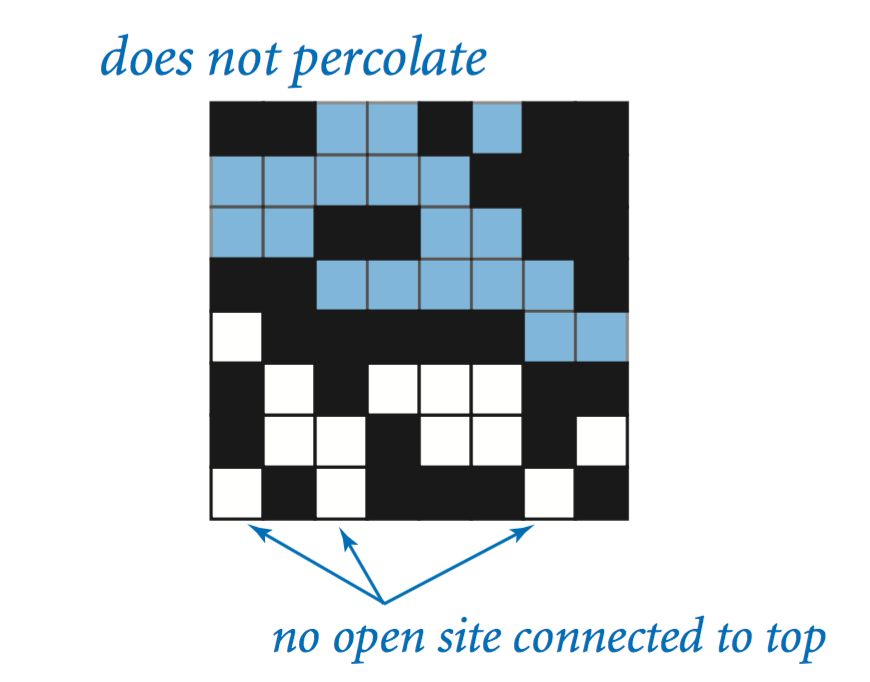
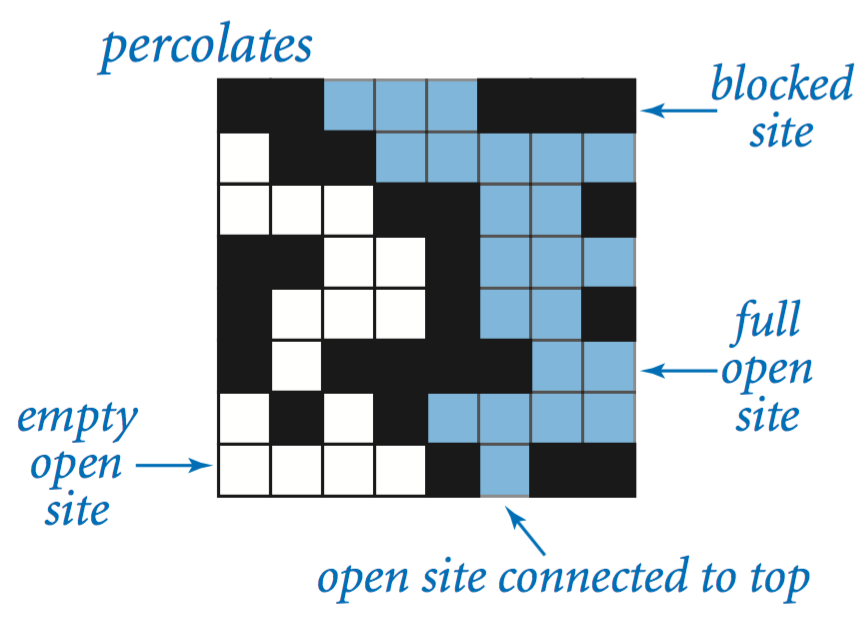
If sites are independently set to be open with vacancy probability p, what is the probability that the system percolates? No mathematical solution to this problem has yet been derived. Our task is to write computer programs to help study the problem.

渗透模型说明(背景)：
         有一个N*N矩阵，如上图，每个小格子代表一个site，当site为black时说明当前site为blocked(关闭的),非黑色为open,当一个site为open且他和其他相邻的site连接并且可以连接到矩阵顶部我们称这个site为full，如果矩阵最底部有site可以连接到矩阵顶部，我们称这个矩阵为渗透的。
参考资料：(百度可找到)

https://www.jianshu.com/p/667e0bb3ef88

https://blog.csdn.net/xiudoushishang/article/details/39519231

 

Data representation.

Our first step is to pick a representation of the data. We use one boolean matrix isOpen[][] to represent which sites are open and another boolean matrix isFull[][] that to represent which sites are full.

Vertical percolation.

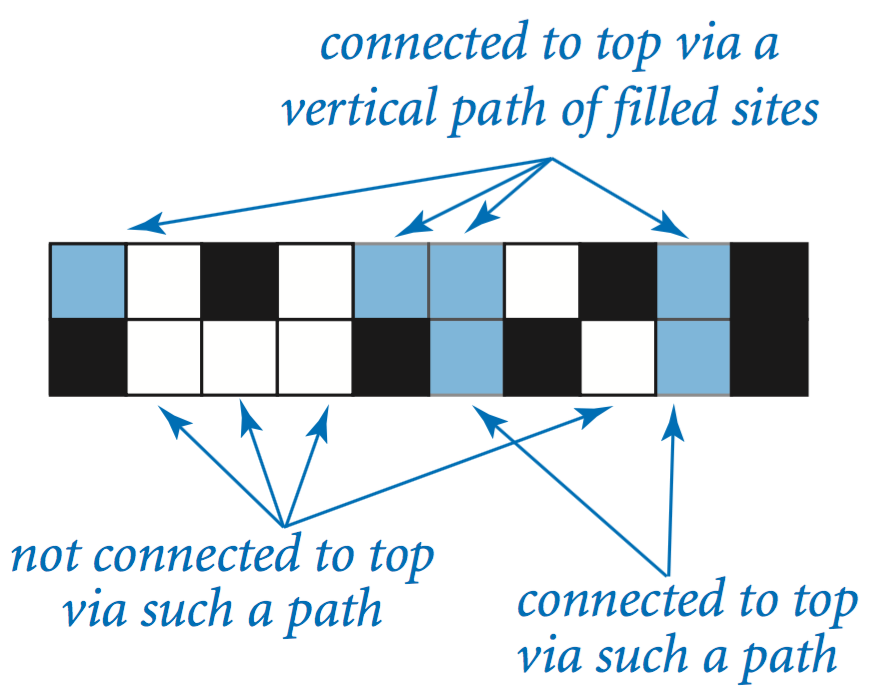
Given a boolean matrix that represents the open sites, how do we figure out whether it represents a system that percolates? For the moment, we will consider a much simpler version of the problem that we call vertical percolation. The simplification is to restrct attention to vertical connection paths.

  VerticalPercolation.java determines the sites that are filled by some path that is connected vertically to the top using a simple calculation.

Data visualization.

PercolationVisualizer.java is a test client that generates random boolean matrices and plots them using standard drawing.

Estimating probabilities.

PercolationProbability.java estimates the probability that a random n-by-n system with site vacancy probability p percolates. We refer to this quantity as the percolation probability. To estimate its value, we simply run a number of experiments.

Recursive solution for percolation.

How do we test whether a system percolates in the general case when any path starting at the top and ending at the bottom (not just a vertical one) will do the job? Remarkably, we can solve this problem with a compact program, based on a classic recursive scheme known as depth-first search. Percolation.java takes this approach. See the textbook for details.

Adaptive plot.

 PercolationPlot.java plots the percolation probability as a function of the site vacancy probability p for an n-by-n system. It uses a recursive approach that produces a good-looking curve at relatively low cost.

           

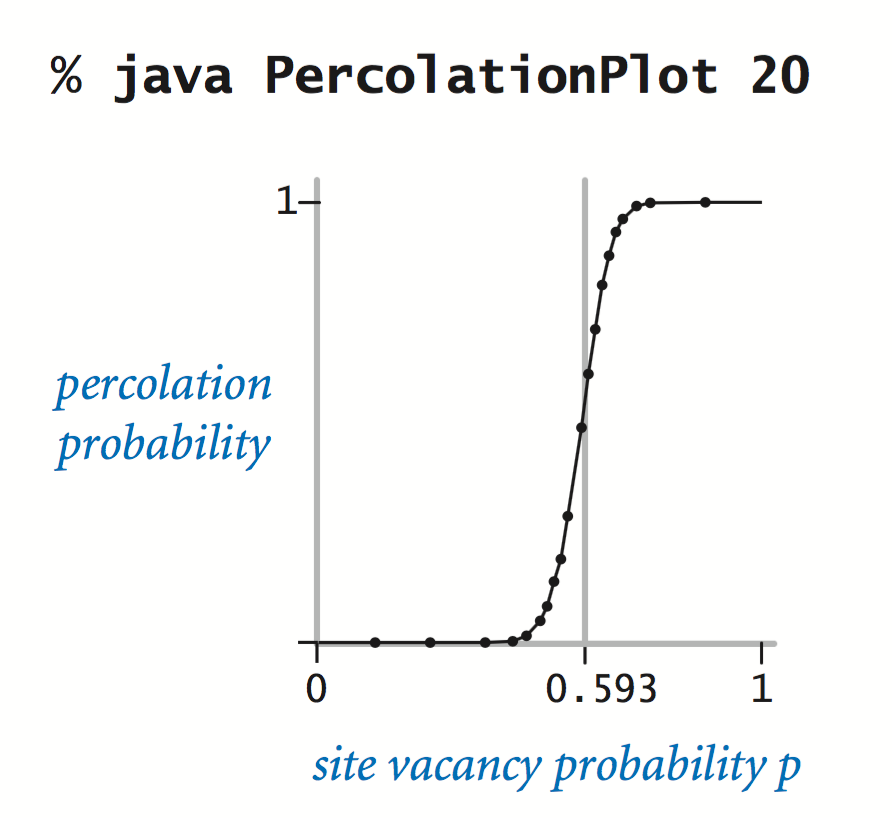
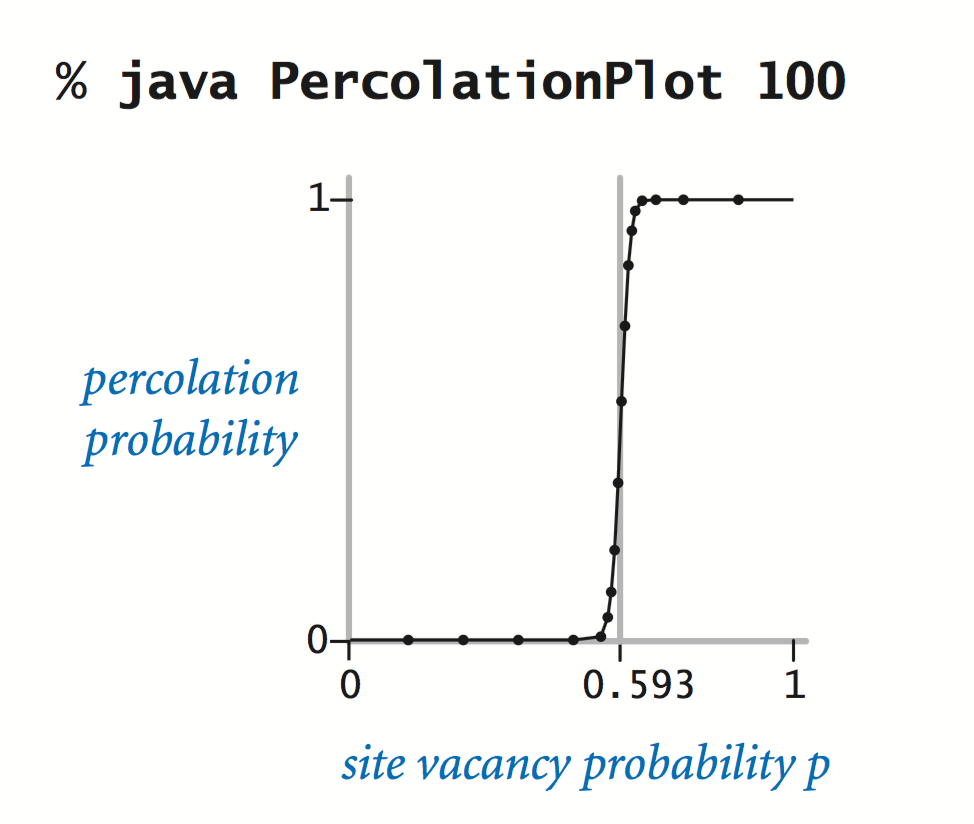
The curves support the hypothesis that there is a threshold value (about 0.593): if p is greater than the threshold, then the system almost certainly percolates; if p is less than the threshold, then the system almost certainly does not percolate. As n increases, the curve approaches a step function that changes value from 0 to 1 at the threshold. This phenomenon, known as a phase transition, is found in many physical systems.