The idea of calling one function from another immediately suggests the possibility of a function calling itself. The function-call mechanism in Java supports this possibility, which is known as recursion.

Your first recursive program.

The "Hello, World" for recursion is the factorial function, which is defined for positive integers n by the equation（第一个递归程序是计算n的阶乘）

$$\mathrm{<span\; style="font-family:\; times\; new\; roman;">n</span>}<span\; style="font-family:\; times\; new\; roman;">!</span><span\; style="font-family:\; times\; new\; roman;">=</span>\mathrm{<span\; style="font-family:\; times\; new\; roman;">n</span>}<span\; style="font-family:\; times\; new\; roman;">\times </span><span\; style="font-family:\; times\; new\; roman;">(</span>\mathrm{<span\; style="font-family:\; times\; new\; roman;">n</span>}<span\; style="font-family:\; times\; new\; roman;">-</span>\mathrm{<span\; style="font-family:\; times\; new\; roman;">1</span>}<span\; style="font-family:\; times\; new\; roman;">)</span><span\; style="font-family:\; times\; new\; roman;">\times </span><span\; style="font-family:\; times\; new\; roman;">(</span>\mathrm{<span\; style="font-family:\; times\; new\; roman;">n</span>}<span\; style="font-family:\; times\; new\; roman;">-</span>\mathrm{<span\; style="font-family:\; times\; new\; roman;">2</span>}<span\; style="font-family:\; times\; new\; roman;">)</span><span\; style="font-family:\; times\; new\; roman;">\times </span><span\; style="font-family:\; times\; new\; roman;">\dots </span><span\; style="font-family:\; times\; new\; roman;">\times </span>\mathrm{<span\; style="font-family:\; times\; new\; roman;">2</span>}<span\; style="font-family:\; times\; new\; roman;">\times </span>\mathrm{<span\; style="font-family:\; times\; new\; roman;">1</span>}$$

The quantity n! is easy to compute with a for loop, but an even easier method in Factorial.java is to use the following recursive function:

public static long factorial(int n) {    if (n == 1) return 1;    return n * factorial(n-1); }

We can trace this computation in precisely the same way that we trace any sequence of function calls.

factorial(5)   factorial(4)      factorial(3)         factorial(2)            factorial(1)               return 1            return 2*1 = 2         return 3*2 = 6      return 4*6 = 24   return 5*24 = 120

Our factorial() implementation exhibits the two main components that are required for every recursive function.

• The base case returns a value without making any subsequent recursive calls.(返回，或终止条件，停止递归) It does this for one or more special input values for which the function can be evaluated without recursion. For factorial(), the base case is n = 1.

• The reduction step is the central part of a recursive function. (递归步骤) It relates the value of the function at one (or more) input values to the value of the function at one (or more) other input values. Furthermore, the sequence of input values values must converge to the base case.(向终止条件收敛) For factorial(), the value of n decreases by 1 for each call, so the sequence of input values converges to the base case.

Euclid's algorithm.

The greatest common divisor (gcd) of two positive integers is the largest integer that divides evenly into both of them. For example, the gcd(102, 68) = 34. (最大公约数)

We can efficiently compute the gcd using the following property, which holds for positive integers p and q:

If p > q, the gcd of p and q is the same as the gcd of q and p % q.

The static method gcd() in Euclid.java is a compact recursive function whose reduction step is based on this property.

gcd(1440, 408)   gcd(408, 216)      gcd(216, 192)         gcd(192, 24)            gcd(24, 0)               return 24            return 24         return 24      return 24   return 24

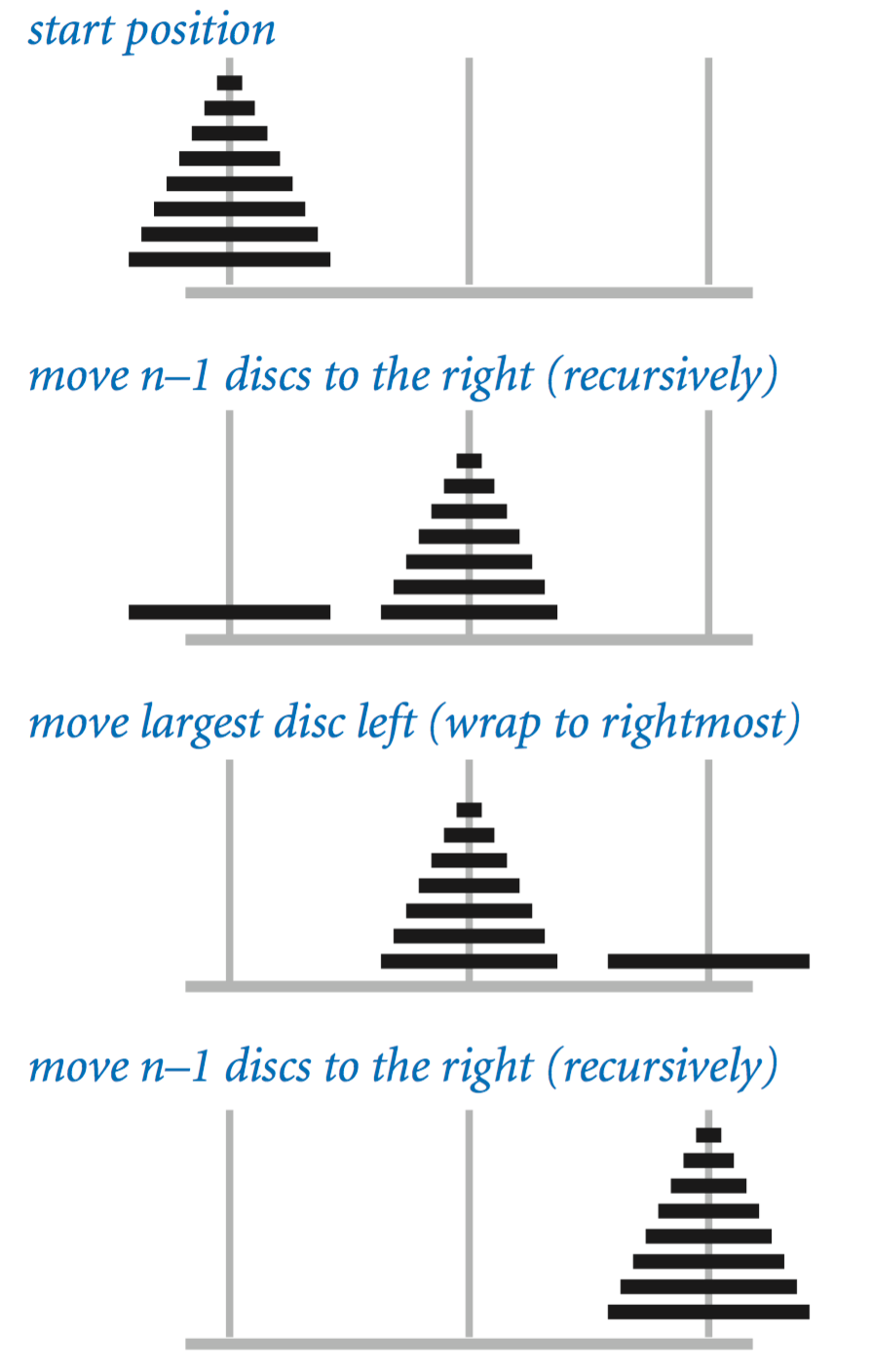
Towers of Hanoi.

In the towers of Hanoi problem, we have three poles and n discs that fit onto the poles. The discs differ in size and are initially stacked on one of the poles, in order from largest (disc n) at the bottom to smallest (disc 1) at the top. The task is to move all n discs to another pole, while obeying the following rules:

• Move only one disc at a time.

• Never place a larger disc on a smaller one.

Recursion provides just the plan that we need: First we move the top n−1 discs to an empty pole, then we move the largest disc to the other empty pole, then complete the job by moving the n−1 discs onto the largest disc. TowersOfHanoi.java is a direct implementation of this strategy.

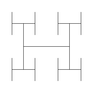
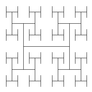
Recursive graphics.

Simple recursive drawing schemes can lead to pictures that are remarkably intricate(复杂). For example, an H-tree of order n is defined as follows: The base case is null for n = 0. The reduction step is to draw, within the unit square three lines in the shape of the letter H four H-trees of order n − 1, one connected to each tip of the H with the additional provisos that the H-trees of order n − 1 are centered in the four quadrants of the square, halved in size. (直接看图片和代码)

Htree.java takes a command-line argument n, and plots to standard drawing an H-tree of order n. An H-tree is a simple example of a fractal: a geometric shape that can be divided into parts, each of which is (approximately) a reduced size copy of the original.

Pitfalls of recursion.

With recursion, you can write compact and elegant programs that fail spectacularly at runtime.

• Missing base case. The recursive function in NoBaseCase.java is supposed to compute harmonic numbers, but is missing a base case: (无限循环)
  

  public static double harmonic(int n) {    return harmonic(n-1) + 1.0/n; }

  If you call this function, it will repeatedly call itself and never return.

• No guarantee of convergence. Another common problem is to include within a recursive function a recursive call to solve a subproblem that is not smaller than the original problem. For example, the recursive function in NoConvergence.java goes into an infinite recursive loop for any value of its argument (except 1).  (不收敛)
  

  public static double harmonic(int n) {    if (n == 1) return 1.0;    return harmonic(n) + 1.0/n; }

• Excessive memory requirements. If a function calls itself recursively an excessive number of times before returning, the memory required by Java to keep track of the recursive calls may be prohibitive. The recursive function in ExcessiveMemory.java correctly computes the nth harmonic number. However, calling it with a huge value of n will lead to a StackOverflowError. （溢出）
  

  public static double harmonic(int n) {   if (n == 0) return 0.0;   return harmonic(n-1) + 1.0/n; }

• Excessive recomputation. The temptation to write a simple recursive program to solve a problem must always be tempered by the understanding that a simple program might require exponential time (unnecessarily), due to excessive recomputation. For example, the Fibonacci sequence

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...

is defined by the formula

$${\mathrm{<span\; style="font-family:\; times\; new\; roman;">F</span>}}_{\mathrm{<span\; style="font-family:\; times\; new\; roman;">n</span>}}<span\; style="font-family:\; times\; new\; roman;">=</span>{\mathrm{<span\; style="font-family:\; times\; new\; roman;">F</span>}}_{\mathrm{<span\; style="font-family:\; times\; new\; roman;">n</span>}<span\; style="font-family:\; times\; new\; roman;">-</span>\mathrm{<span\; style="font-family:\; times\; new\; roman;">1</span>}}<span\; style="font-family:\; times\; new\; roman;">+</span>{\mathrm{<span\; style="font-family:\; times\; new\; roman;">F</span>}}_{\mathrm{<span\; style="font-family:\; times\; new\; roman;">n</span>}<span\; style="font-family:\; times\; new\; roman;">-</span>\mathrm{<span\; style="font-family:\; times\; new\; roman;">2</span>}}\text{<span style="font-family: times new roman;"> for </span>}\mathrm{<span\; style="font-family:\; times\; new\; roman;">n</span>}<span\; style="font-family:\; times\; new\; roman;">\ge </span>\mathrm{<span\; style="font-family:\; times\; new\; roman;">2</span>}<span\; style="font-family:\; times\; new\; roman;">,</span>\text{<span style="font-family: times new roman;"> with </span>}{\mathrm{<span\; style="font-family:\; times\; new\; roman;">F</span>}}_{\mathrm{<span\; style="font-family:\; times\; new\; roman;">0</span>}}<span\; style="font-family:\; times\; new\; roman;">=</span>\mathrm{<span\; style="font-family:\; times\; new\; roman;">0</span>}\text{<span style="font-family: times new roman;"> and </span>}{\mathrm{<span\; style="font-family:\; times\; new\; roman;">F</span>}}_{\mathrm{<span\; style="font-family:\; times\; new\; roman;">1</span>}}<span\; style="font-family:\; times\; new\; roman;">=</span>\mathrm{<span\; style="font-family:\; times\; new\; roman;">1</span>}$$

A novice programmer might implement this recursive function to compute numbers in the Fibonacci sequence, as in Fibonacci.java:

// Warning: spectacularly inefficient. public static long fibonacci(int n) {    if (n == 0) return 0;    if (n == 1) return 1;    return fibonacci(n-1) + fibonacci(n-2); }

However, this program is spectacularly inefficient! To see why it is futile to do so, consider what the function does to compute fibonacci(8) = 21. It first computes fibonacci(7) = 13 and fibonacci(6) = 8. To compute fibonacci(7), it recursively computes fibonacci(6) = 8 again and fibonacci(5) = 5. Things rapidly get worse. The number of times this program computes fibonacci(1) when computing fibonacci(n) is precisely F_n.

//f1是第n-1个Feibonacii数，f2是第n-2个Fibonacci数，n是所需Fibonacci序列的第n个数
long Fibonacci(long f1,long f2,long n) {
 if (n < 3)
  return f1;
 else
  return Fibonacci(f1 + f2 , f1 , n - 1);
}

调用：Fibonacci(1, 1，n)