主要内容

◆即期利率和短期利率

◆短期利率和收益率曲线斜率

◆从即期利率(到期收益率)推算未来短期利率

◆根据观察到的收益率解出远期利率

◆利率的不确定性

即期利率和短期利率

即期利率（spot rate）：零息债券到期收益率被称为即期利率，意思是，在当前时刻、未来会持续一段时间的利率。

短期利率（short rate）：在一定区间内（例如一年）不同时点均适用的利率。

在前面的例子中，今天的短期利率为5%，下一年的短期利率为7.01%。

即期利率是短期利率的几何平均。

如图： 短期利率和即期利率

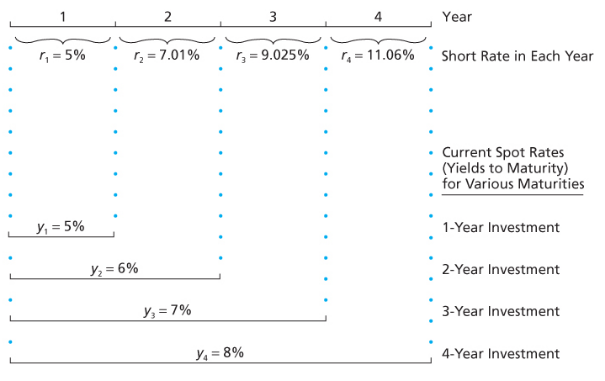
短期利率和收益率曲线斜率

当下一年度短期利率r2 大于今年的短期利率r1时， 收益率曲线向上倾斜。

——暗示收益率预计会上升。

当下一年的短期利率r2 小于今年的短期利率r1时， 收益率曲线会下降。

——暗示收益率预计会下降。

从即期利率(到期收益率)推算未来短期利率

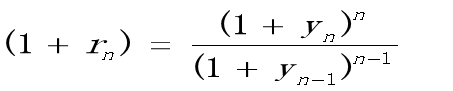
当未来利率不确定时，无法推断未来“确定”的短期利率。因为不确定性，我们将10.3推断出来的利率称为远期利率(forward interest rate)，而非未来短期利率(future short rate)。

根据观察到的收益率解出远期利率

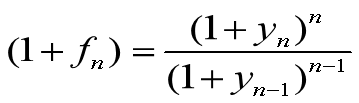
fn = n期的远期利率

yn = n期债券在第n期的到期收益率

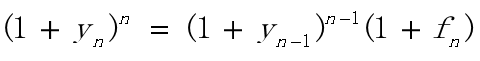
计算远期利率

例：假设远期利率与未来短期利率是相等的，4年期利率= 8%，3年期利率= 7%。

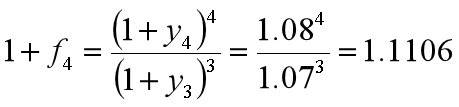
利率的不确定性

假设今天的利率是r1=5% ，下一年的期望短期收益率是E(r2)=6%，两年期零息债券的价格：

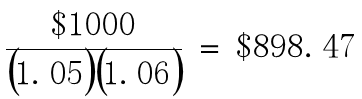
一年期零息债券的价格:

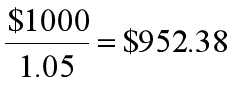
只希望投资一年的短期投资者

购买2年期债券，在第一年的年底以$1000/1.06 =$943.40的价格卖出或者购买1年期债券持有至到期。

但是两年期债券的收益率是有分险的。

如果下一年的利率大于（或小于）6%呢? 

债券的价格将低于（或高于）$943.40。

因为有风险，两年期债券的售价应该要低于我们忽略风险所计算出来的$898.47。

持有长期债券的投资者将会要求更高的风险溢价。

这种流动性溢价补偿了短期投资者在将来出售时的不确定性。