主要内容

多因素模型中β与风险溢价的性质

根据多因素证券市场线原理，基于GDP和利率的两因素模型的期望收益包括三部分：

⑴无风险收益率。

⑵ 承担了GDP这个系统宏观风险因素应享有的风险溢价。

⑶承担了利 率这个系统宏观风险因素应享有的风险溢价。

包括GDP和利率两因素的证券市场线为：

 

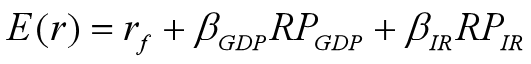
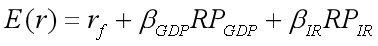
表示证券收益对GDP增长非预期变化的敏感性；

是“单位”GDP风险的风险溢价；

表示证券收益对利率非预期变化的敏感性；

是“单位”利率风险的风险溢价。

可见，在证券收益的表达式中β表示证券收益对风险因素未预期到的变化的敏感性，可以通过对大量历史数据进行回归分析，获取一个β的估计经验值;

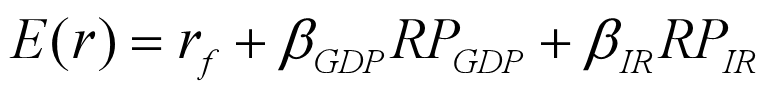
多因素模型相较于单因素模型的一个突出优势就是对证券收益的描述更贴近实际、更丰富、也更直观。

单因素模型将影响证券收益的风险因素笼统定义为一个系统宏观风险因素，难以识别影响收益的具体系统宏观因素及分别对证券收益的不同影响程度。

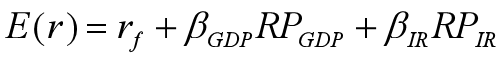
多因素模型能明晰、识别影响证券收益的各个具体的系统宏观风险因素、不同影响程度及各个因素风险溢价的性质（可为负）。

从而，为较好地管理投资组合的风险提供了技术和工具。

以利率风险为例

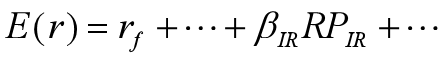
利率β具有负的性质。因为利率上升意味着全社会融资成本上升。但是，不同行业的利率风险溢价具有不同正负性质，于是对证券收益产生着不同的影响。

对一般企业来说：

若贷款利率上升，一般企业财务成本加大，较之前经营风险明显上升，要保持原有业绩就必须要求更高的风险补偿，故一般企业的利率风险溢价就具有正的性质，因而利空基本面。

 

上式表明：对一般企业来说，利率风险对期望收益的贡献为负，即一个负的利率因素β乘以一个正的利率风险溢价得到一个负数，降低业绩预期。

对银行业来说：

若存贷款不对称加息，存款利率不变，贷款利率上升，银行业利息收益扩大，实际上其经营风险在下降，要保持原有业绩可以允许低一点的风险补偿，故银行业的利率风险溢价具有负的性质，反而利多基本面。

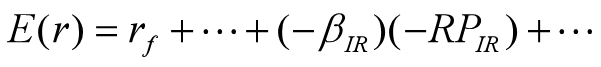
上式表明：对银行业来说，利率风险对期望收益的贡献为正，即一个负的利率因素β乘以一个负的利率风险溢价得到一个正数，调升业绩预期。

在一个加息或利率上升周期，配置利率风险溢价为负的行业资产是对抗、管理利率风险的有效方式。

以汇率风险为例

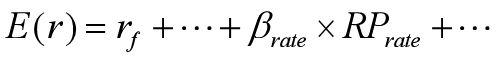
汇率β具有负的性质，因为通常本币汇率上升会利空本国经济基本面。但是出口商和进口商的汇率风险溢价却不同，出口商汇率风险溢价为正，而进口商汇率风险溢价为负，因此本币汇率变动会形成对出口商与进口商不同的业绩冲击。

对出口商来说：

原汇率为1︰10

出口商在国内6元成本生产一双鞋，出口美国换1美元，回国内换成10元，赚4元人民币。

现汇率为1︰5

升值后，出口一双鞋换1美元，回国后只能换为5元人民币，亏损1元人民币。

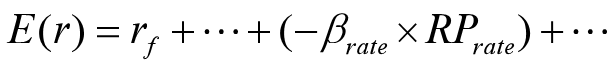
人民币升值，对出口商不利，承担的经营风险增大，要求的风险溢价上升，故出口商汇率风险溢价为正，负的汇率β乘正的风险溢价，调降业绩预期。

对进口商来说：

原汇率为1︰10

进口商以10元换1美元，从美国进口一双鞋，在国内卖12元人民币，赚2元人民币。

现汇率为1︰5

升值后，进口商10元能换2美元，可进口两双鞋，一双卖12元，可卖24元，赚14元。

人民币升值，对进口商有利，承担的经营风险降低，要求的风险溢价下降，故进口商汇率风险溢价为负，负的汇率β乘负的风险溢价，调升业绩预期。

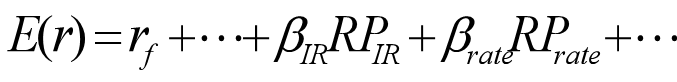
小结：

一是要积极优先配置与β具有相同正负性质的因素风险溢价的行业资产。

二是可以主动接受一个看起来低回报率的资产，但是这是基于其系统因素风险拥有一个负的风险溢价。