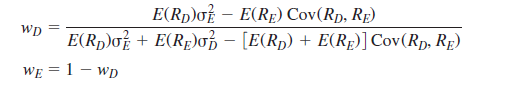主要内容

◆风险的分类

◆分散风险

◆构建最优风险资产组合

风险的分类

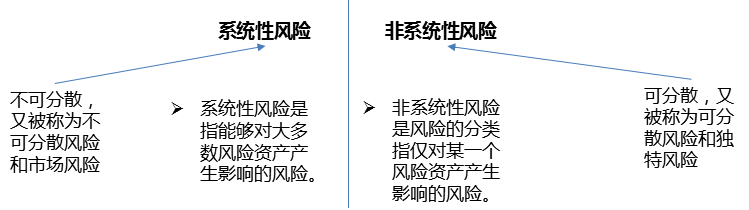
风险资产组合的定义：

将资金按一定比例投资于若干种风险资产，从而达到提高投资资金收益，降低资金风险的目的。

通过构建风险资产组合可以有效的分散组合中的非系统风险，但是无法分散系统性风险。

分散风险

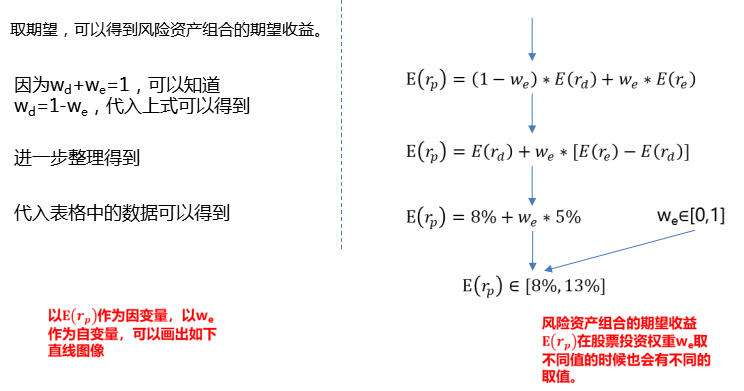
1、风险资产组合期望收益变化

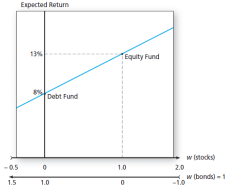
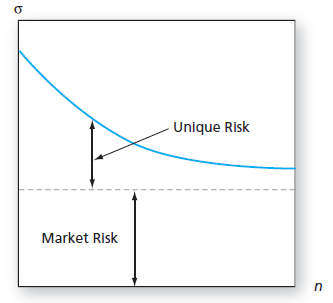
2、风险资产风险变化

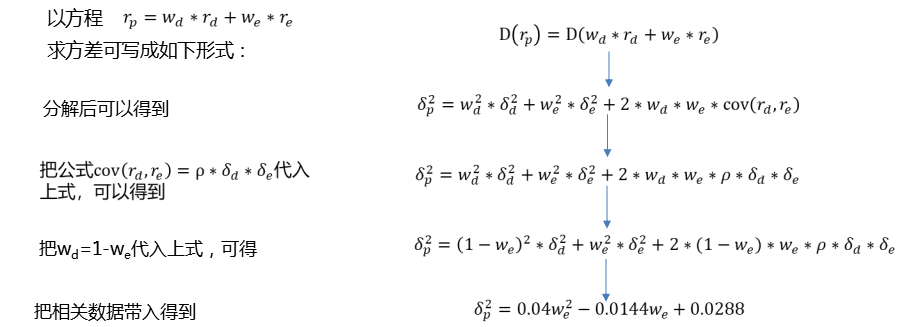
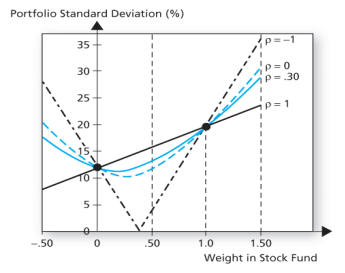
当把资金的18%投入股票，剩余82%投入债券时，整个资金所面对的风险最小，仅有11.45%，小于只投资于债券的12%，更小于只投资于股票的20%，这就是分散风险。

必须记住，分散的是非系统性风险

构建最优资产风险

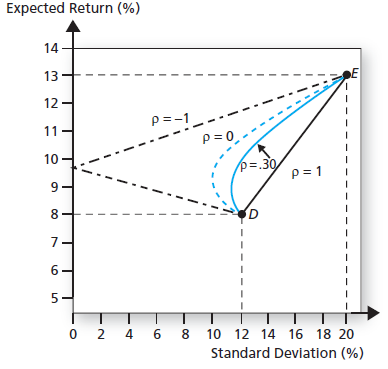
  该图的每一个点都表示在既定的相关系数下两种资产的期望收益与风险的配比关系，注意每一个配比关系下都对应着投资组合的权重，我们把这些线称为在既定相关系数下的投资组合可行集。

构建最优资产风险

在既定的相关系数下，到底哪一个点是最优的资产组合点呢，能够让风险最小的点是最优点吗？如下图的点A。

在可行集上任意找一个点，建立与无风险收益点的连线，就构成了资本配置线（CAL），而资本配置线的斜率被称为夏普比率，我们认为夏普比率越大越好，这样很自然的就可以知道相切是使夏普比率最大的方式，如下点p是我们认为最优的风险资产组合点，因为它是在可以获得的组合可行集里面能让夏普比率最大的点。

 

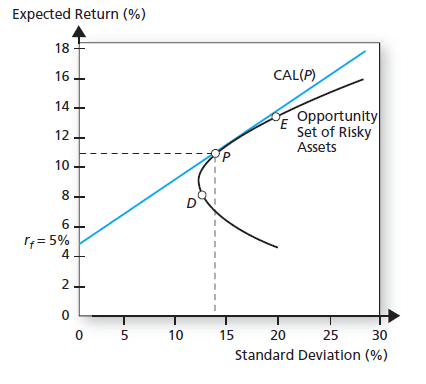
求p点所对应的投资权重，则可以使用既定公式：