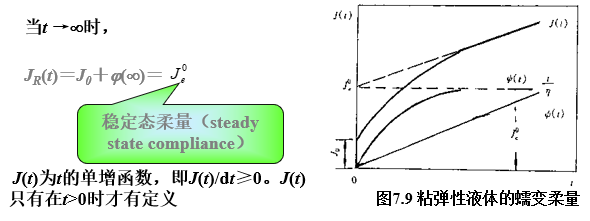
剪切蠕变柔量J(t)是由材料性质决定的，它反映材料的内部结构.在蠕变实验中，应变是随时间增大的，因此可以认为

J(t)是随时间单调增加的，即J(t)/dt≥0

7.3.1 粘弹性固体

对粘弹性固体，当瞬时地加上一个应力时，它产生一个瞬时的弹性应变，然后应变随时间逐渐发展，并趋于一个极限值。其J(t)的一般形式

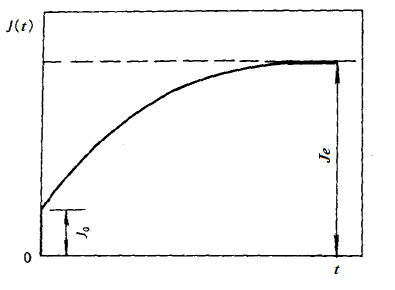
            图7.8 粘弹性固体的蠕变柔量

J0称为瞬时剪切模量。J0反映粘弹性固体的线弹性变形，定义为

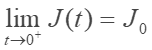
Je为时间相当长后J(t)的趋近值，称为平衡柔量（Equilibriumcompliance）

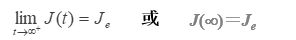
J(t)由两部分组成，即

J(t)＝J0＋j(t)

j(t)称为推迟剪切柔量（Delayedshear compliance），它是时间t的单调增加函数。当t →¥时：

f(t)反映橡胶弹性，因而是可以恢复的

7.3.2 粘弹性液体

可把粘弹性液体的蠕变柔量表示为

J(t)＝J0＋j(t)＋t/h

式中，t/h表示粘性流动，J0＋f(t)为可恢复的弹性变形，可用JR(t)表示

J(t)＝JR(t)＋t/h