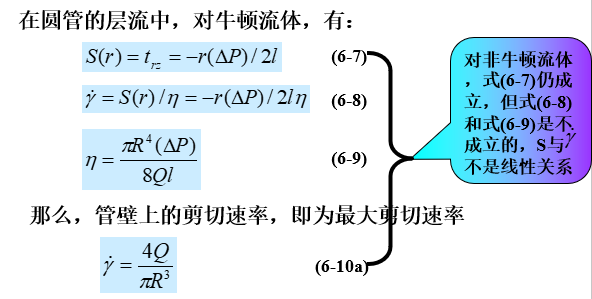
要用毛细管粘度计测定非牛顿流体的粘度，Weissenberg提出一种进行校正的方法。定义熔体通过毛细管的表观剪切速率等于管壁上的剪切速率

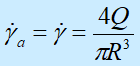(6-10b) 

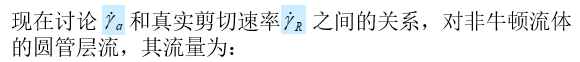
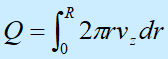
式中，vz为r的函数，对上式进行分部积分：

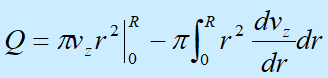
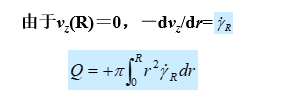(6-13) 

再进行换元，即

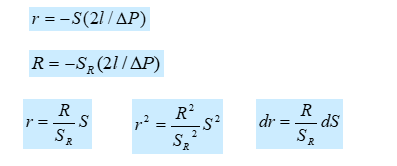
SR为在管壁处的剪切应力，将以上代入式(6-13)：

(6-14) 

将式(6-14)代入式(6-10b)

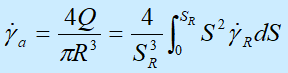 (6-15)

对积分上限求导。得：

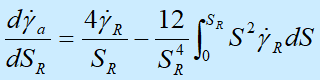(6-16) 

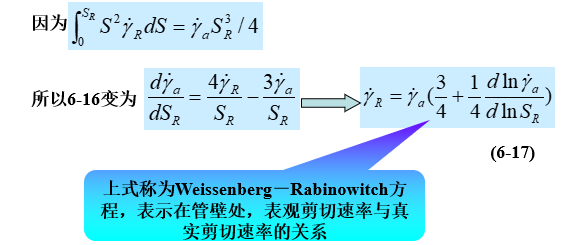
由上分析可见，对非牛顿流体的Poiseuille（圆管中的层流）流动，Hagen- Poiseuille方程应由式(6-13)代替。流速的分布也是椭圆分布，对假塑性的非牛顿流体，椭圆变平；而对膨胀性的非牛顿流体，则椭圆变尖。在极端情况下变为三角形

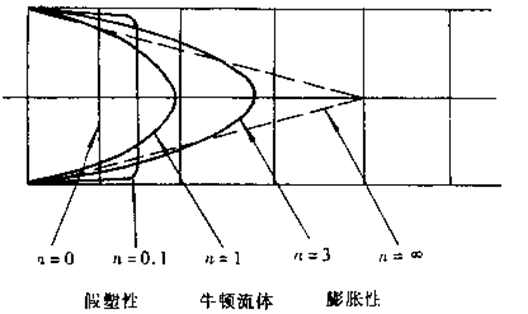
           Poiseuille流动中的流速分布