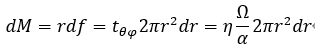4.3.1圆管中流体的稳定层流（Laminar flow）

假定流动是稳定的．即流体内每个质点的流动速度不随时间变化

采用柱坐标（r，q，z）而不用直角坐标，我们这样定义r，q，z。即z轴与圆管的轴一致，r与z轴垂直

层流流动或称Poiseuille（泊肃叶）流动，是指流体仅沿z轴方向流动，没有沿r或沿q方向的流动。即

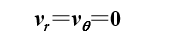
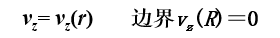
上两式说明层流流动可看作圆管中许多无限薄的同心圆柱状流体薄层的流动

设圆管长为l，我们来讨论离轴r的一层圆柱状流体，在其外表面的流体对其施加的剪应力为trz，总力为：

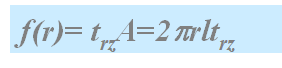
A为圆柱体表面的面积，f(r)为流动的阻力。为了保持稳定的层流流动，必须对圆管两端面的流体施加压力差△P，总力为(△P)pr2使得：

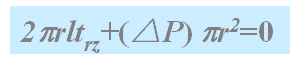
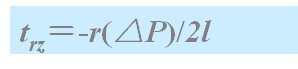
可见，如果层流流动是稳定的，剪切应力是r的线性函数，如果流体是牛顿流体，则剪切应力正比于剪切速度，即

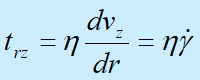
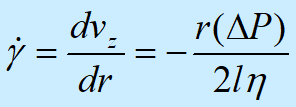
用边界条件vz(R)＝0解上列方程，有

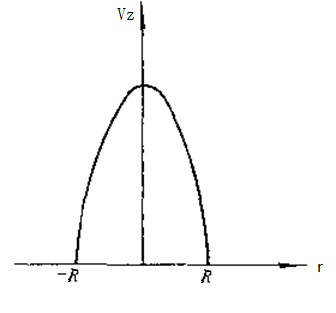                        速度分布                    剪切速率

圆管中的层流流动的流速分布为一椭圆函数，而速度梯度即剪切速度则是r的线性函数。在圆管的轴心处vz具有最大值，而dvz/dr为零，在管壁处则相反，vz＝0，而dvz/dr具有最大值

通过从r到r+dr的环状圆柱体的流体流量（单位时间流过的流体体积）为

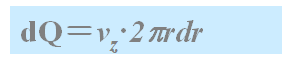
通过整个截面的流量为

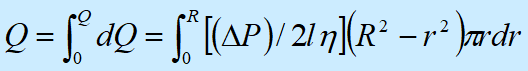
积分得

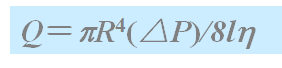Hagen-Poiseuille（哈根－泊肃叶）方程

4.3.2 Couette（库爱特）流动－同轴环隙中的旋转流动

Couette流动，是指在外圆筒和内圆筒之间环形部分内的流体中的任一质点仅围绕着内外管的铀以角速度w（rad/s）作圆周运动，没有沿z或r方向的流动。w仅与r有关而与q和z无关，即

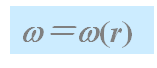
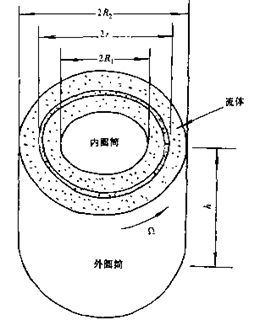仍采用圆柱坐标r，q，z，z轴为内外管的轴向。由于只存在绕轴的圆周运动，所以trz=tqz=0，只存在一个剪切应力trq=tqr

剪切速度为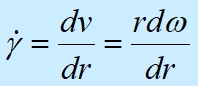

要保持这一流动，对离轴r的流体层必须施加扭矩M(r)：

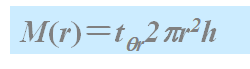
式中，h为内外圆筒的高度，设流体为牛顿型的，内圆筒固定，外圆筒以角速度W旋转，用柱坐标的动量方程，可推导出环隙内流体沿径向的周向速度，它为：

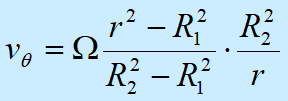
角速度: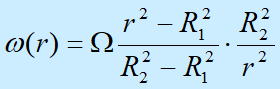

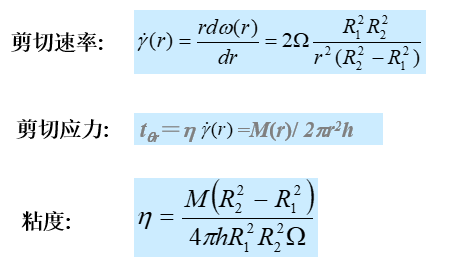
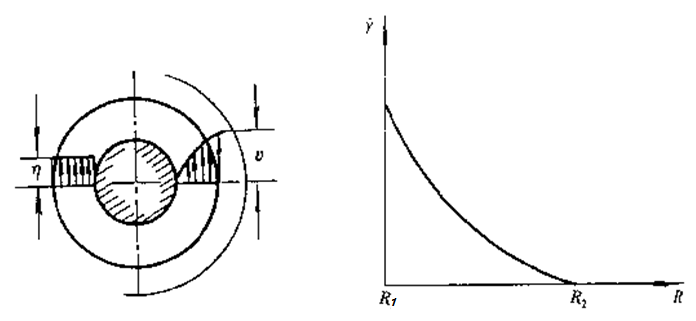
   Couette 流动中的速度分布        Couette 流动中的剪切速率

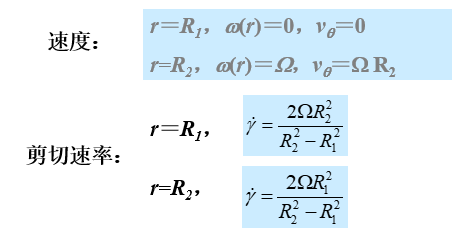
4.3.3扭转流动（Torsional flow）

扭转流动发生在两个平行的圆盘之间。圆盘的半径为R。两圆盘之间的距离为h。上圆盘以角速度W旋转，施加的扭矩为M。

                                    扭转流动

对扭转流动采用柱面坐标进行分析。非零剪切应力分量为tzq，作用在z面上，方向为q方向，即切线方向。在扭转流动中，只有q方向的流动，即

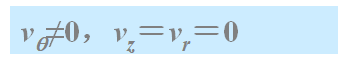
vq随z坐标变化，因此，剪切速率为

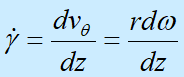
式中，w为角速度。扭转流动中的剪切速率为

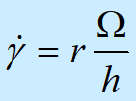即为r的线性函数

求角速度w可用下式：

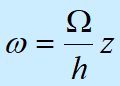即w为z坐标的线性函数，但与r坐标无关

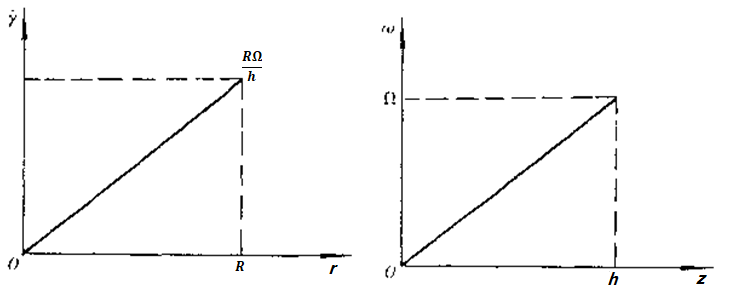
  图       扭转流动中的剪切速率          图  扭转流动的角速度

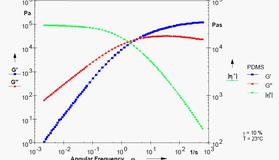
分析扭转流动中M与W的关系。由于剪切速率与r坐标有关，因此剪切应力也与r有关

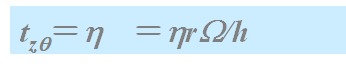
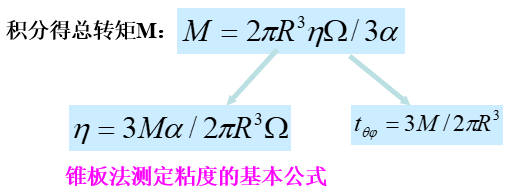
4.3.4锥板流动（Cone and plate flow）

锥板流动发生在一个圆锥体与一个圆盘之间，圆锥与平板之间的夹角a很小，一般小于40。通常圆锥体以角速度W旋转，它的轴与圆盘垂直，也是圆锥体的旋转轴。圆锥体的顶点与圆盘平面接触

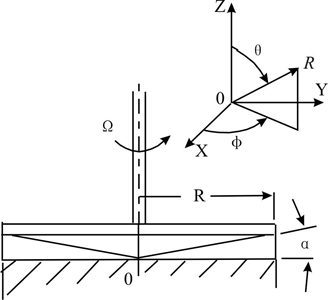对锥板流动，采用球面坐标（r，q，j）进行分析。在锥板流动中，剪切面为具有相同q坐标（圆锥角）的圆锥面（q面）。速度梯度方向为q方向。流体流动的力向为j方向，即切线方向，用w表示，它是q坐标的函数：

在圆锥体表面：q＝p/2-a，w＝W

在平板表面：q＝p/2，w＝0。

剪切速率定义为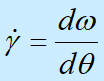

a<40时，可近似地把锥板之间的流动认为是简单剪切流动，即角速度w是q坐标的线性函数：

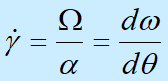
积分得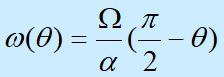

角速度W与转矩之间的关系。在锥板流动中，剪切力作用在q面上，方向为j方向，因此，应力分量为tqj，根据牛顿定律

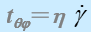
转矩是r的函数，从r到r＋dr的圆锥面上的圆环上的剪力为：