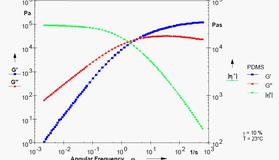
3.3.1 弹性模量谱

聚合物与其他材料相比，其很明显的特点是它们的弹性模量范围很宽（在室温时），因此用途广泛

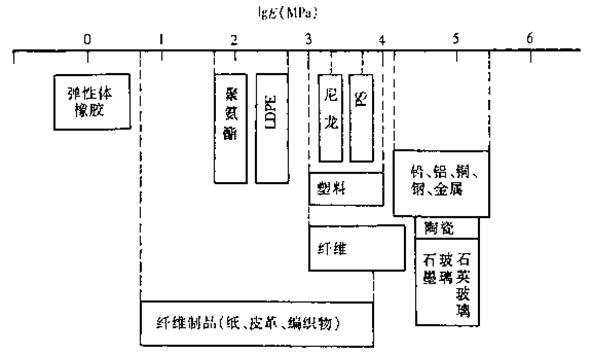
v玻璃态高聚物的弹性模量为103～105  MPa数量级，如：

酚醛塑料：E＝104MPa

密胺塑料：E＝1.4×105MPa

聚氯乙烯(硬质)：E＝4.9×103MPa

v橡胶和弹性体的模量为0.1～1MPa，比玻璃态聚合物低3～4个数量级。

3.3.2聚合物弹性模量与温度的关系 

温度对体积模量的影响较小，低于玻璃化温度和高于玻璃化温度的K相差仅两倍左右，在同一数量级上。拉伸和剪切模量的温度依赖性则很大

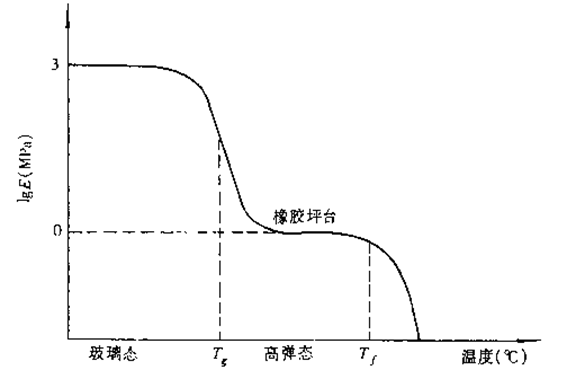
                                  无定形线形聚合物的拉伸模量与温度的关系

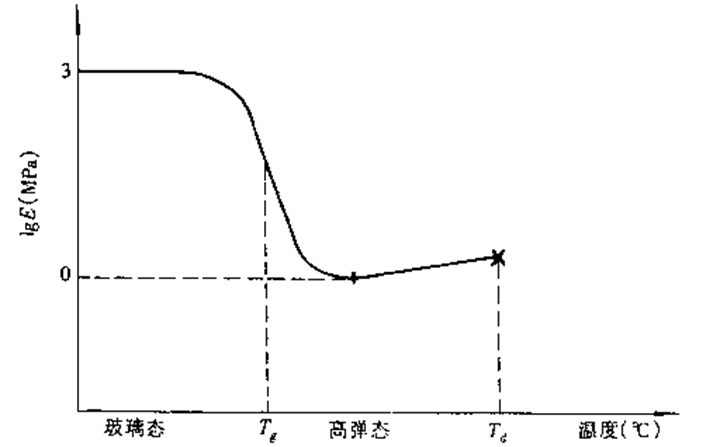
                 交联聚合物（橡胶）的拉伸模量与温度的关系

分子链热运动加强，回缩力逐渐变大，弹性形变能力变小，表现为弹性模量随温度升高而增大

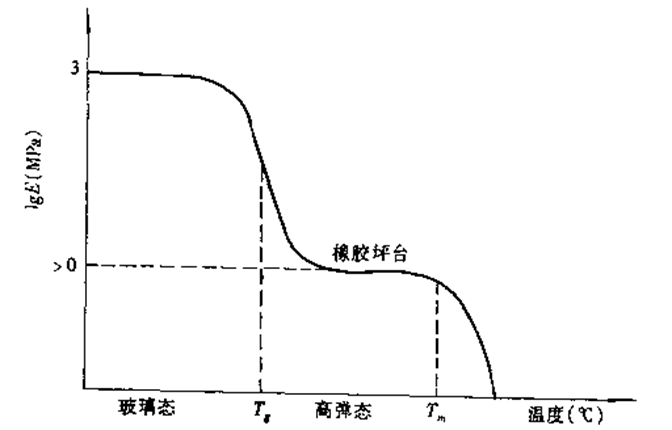
      结晶性线形聚合物的拉伸模量与温度的关系

其形状与无定型聚合物类似，其区别是坪台区较宽，且坪台处的模量较高

3.3.3 模量的分子量依赖性  

  无定型线形聚合物的拉伸模量与分子量的关系（A<B<C）

分子量对模量的影响主要在高弹态和粘流态。分子量越高，橡胶坪台区越宽，但坪台区的模量数量级不因分子量增大而变化，玻璃化温度也保持不变

3.3.4 交联度对拉伸模量的影响

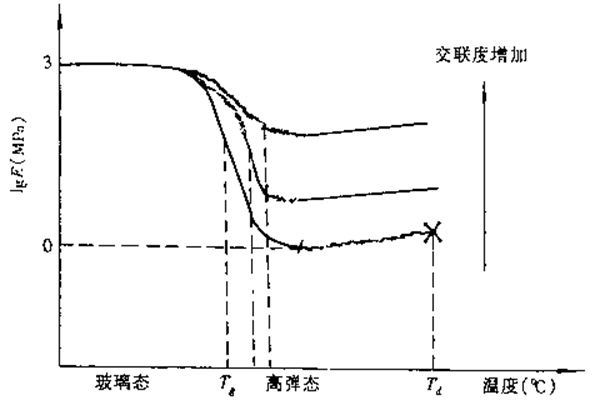
  交联聚合物（橡胶）的拉伸模量与交联度的关系

随着交联度上升，橡胶坪台模量上升，交联度上升至形成网状结构时，E几乎保持不变直到超过分解温度时发生分解。同时玻璃化温度也随交联度提高而上升，而且玻璃化转变区加宽（Tg升高）

3.3.5 结晶度的影响 

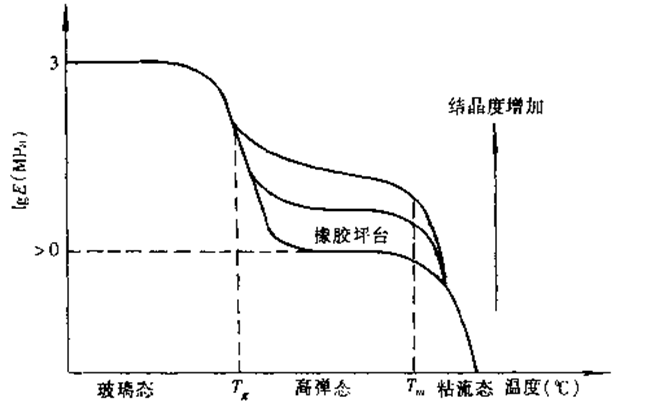
     结晶性线性聚合物的拉伸模量与结晶度的关系

随着结晶度的提高，在低温没有影响，橡胶坪台升高，结晶起交联作用。Tg不受结晶度影响