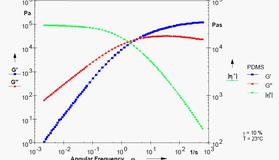
7.2.1正比性

  对于线弹性体，柔量J为材料的性质，与应力大小无关，如图7.3a所示，并与时间无关

q对线性粘弹性体，我们同样要求应变与应力成正比，即

   e(t)=s0J( t)                                            (7-8)

   J(t)=e(t)/s0                                          (7-9) 

这种关系应在任何时刻都成立，J(t)是由材料的性质决定的，与应力的大小无关，如图7.3b所示，s0改变时，J(t)并不改变。我们把材料的性质符合式(7-8)的叫做正比性，但这不是线性粘弹性的准一要求

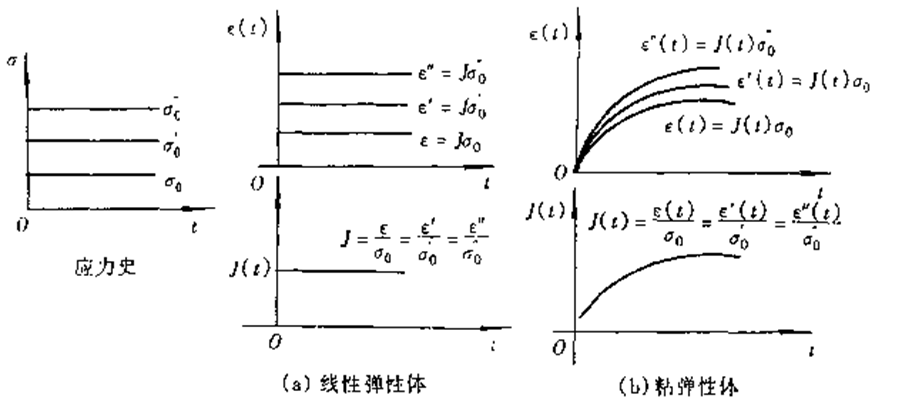
                图7.3正比性

7.2.2加和性

（1）应力史的影响

分析应力s0有不同历史的情况，即应力s0是在不同时刻施加的，如下图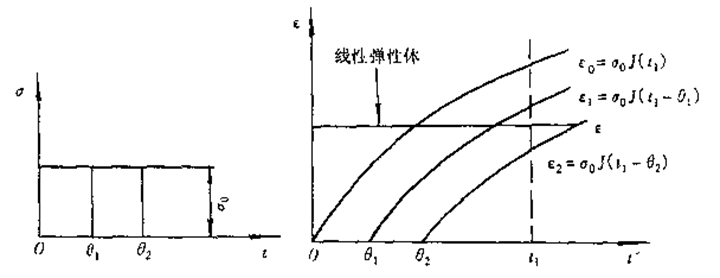

          图 7.4 应力史的影响

假定应力史有三种不同的情况，即应力s0是在时刻零时、q1和q2时施加的，对线性弹性体，相对这三种不同的应力史，应变e＝Js0，即它与应力史无关，只决定于在该时刻的应力s0

对粘弹性材料，如应力史为零时刻施加的：

e0(t)=s0J( t)                                          (7-10)

加应力q1和q2时刻施加的：

e1(t)=s0J( t－q1)                                    (7-11)

e2(t)=s0J( t－q2)                                    (7-12)

在时刻t1时，相应于三种不同应力史，应变e0和e1，e2不同。也就是说，对粘弹性材料，应变史不仅决定于应力的大小，还决定于应力的历史。或者说在某个时刻的应变，不仅决定于该时刻的应力，还决定于此时刻之前所受应力的情况

（2）两步应力史

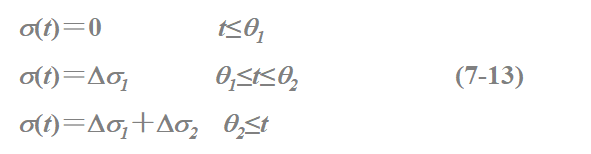
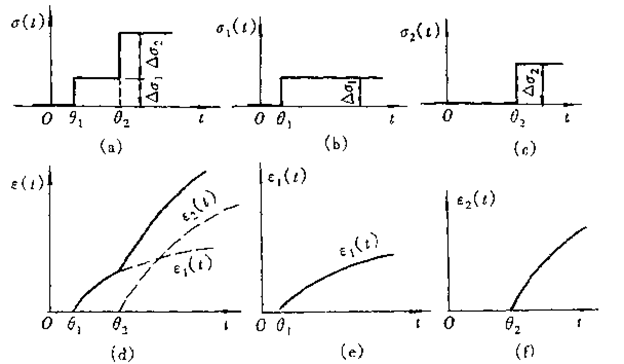
           图7.5 加和性

Ds1和Ds2常数，q2>q1。把它看成是两个应力史之和（见图b和c），即

e(t)＝0                                               t≤q1                  (7-18a)

e(t)＝Ds1J( t－q1)                           q1≤t≤q2            (7-18b)

e(t)＝Ds1J( t－q1) +Ds2J( t－q2)   t≥q2                  (7-18c)

说明应变史是各个独立的应力史产生的相应的应变史的加和，因此可以说该材料的应变具有加和性，这是线性粘弹性的另一个条件

（1）对于任意的应力史，在给定的现在时刻t，应变史是所有应力史的函数。这里t是常数，而q是变量，Ds是随q而变的

（2）当q1＝q2时，即Ds1和Ds2是同时从q1施加时，正比性才适用，即

e(t)＝Ds1J(t－q1) +Ds2J(t－q2)=( Ds1+Ds2) J(t－q1)

（3）在给定的时刻t，应变e(t)并不决定于在该时刻的应力Ds，而是决定于在时刻t之前的全部应力史。举例来说，设在时刻t时，应力为Ds1+Ds2，但可能有不同的应力史，如下图所示。虽然在时刻t1时，应力都是s1+Ds2，但由于它们有不同的应力史，在时刻t1的应变就不同：

e1(t) =( Ds1+Ds2) J(t)

e2(t)＝Ds1J( t) +Ds2J( t－q1)

e3(t)＝Ds1J( t－q1) +Ds2J( t－q2)

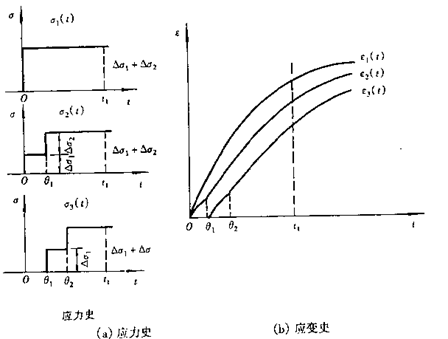
         图7.6 不同应力史的两步应力实验

(3) 连续的应力史

如果应力史是一个任意的随时间而变的函数s(q)，如图所示，在时刻t时的e(t)应是在t之前全部应力史的函数。可近似地把连续的应力史看成是多步的负荷，即在q1时，加Ds(q1)；在q2时，增加一个负荷Ds(q2)，q3时；加Ds(q3)，……在qi时加Ds(qi)，这时

e(t)＝Ds(q1)J( t－q1) +Ds(q2) J( t－q2)+ Ds(q3) J( t－q3)+…….+ Ds(qi) J( t－qi)+……Ds(qm) J( t－qm)=

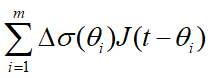
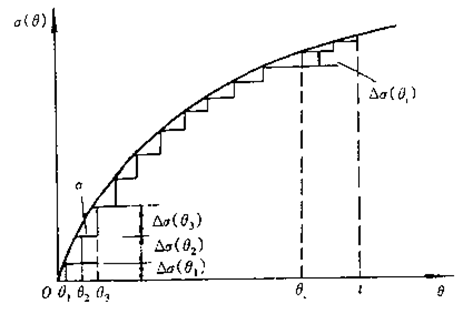
                    图7.7 连续的应力史