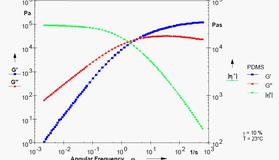
橡胶弹性的唯象理论是从实验现象出发建立描述橡胶的一般性质的数学表示式，而不涉及其分子结构，其主要目标是寻找描述橡胶性质的方便途径，而不是为相应的物理或分子意义提供解释或说明，目前已发展了多种形式的唯象理论，其中用得较多的有Mooney-Rivlin理论和Ogden理论。本章主要讨论橡胶弹性的应力应变关系——Mooney-Rivlin理论

5.2.1变形

        在线弹性的拉伸试验中，应变定义为△l/l，长度的分数变化,这里没有明确式中的l是指原始长度l0还是变形后的长度lf。由于在线弹性中应变是很小的，所以△l/l0与A△l/lf的差别是很小的。

  在橡胶弹性中，应变是很大的，所以必须指明e的定义式是△l/l0还是△l/lf，实际上这两种表示法都可用，也有用别的方法表示应变的。在非线性弹性中，常常使用拉伸比l来表示拉伸试验中的变形

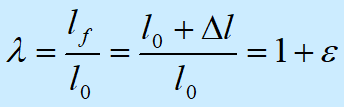
5.2.2应力

线弹性中，定义应力为f /A，这里A也没指明是原始面积A0。还是变形后的面积Af，因为A0与Af在线弹性中是很接近的。

橡胶弹性中，A0则与Af相差较大。实际应力应为f /Af，但由于A0易于测定，习惯上还是采用f /A0为应力，称为工程应力。

5.2.3Mooney-Rivlin理论

线弹性理论的基础是应力是应变的线性函数。在橡胶弹性中应力与应变的关系是非线性的。如果偏离线性较小，有些非线性理论认为应力与应变的关系为二次或三次方程。然而橡胶弹性也不符合这种关系。

对于任意变形的物体．产生变形所需的能量只是变形的函数，在线弹性中有

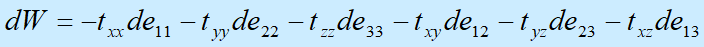
不管变形的性质也不管变形如何复杂，变形物体内任一点的W(应变储能函数)可表示为三个参数l1、l2、l3，（称为基本拉伸比）的函数：

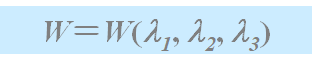
l1、l2、l3表示三个互相垂直方向上的拉伸比。在线弹性中应力可表示为自由能对应变的偏导数，同样在非线性弹性的一般理论中，应力也可表示为应变储能函数W对拉伸比l的偏导数，原则上可由实验来确定W，从而从进一步的实验计算应力

Mooney在橡胶弹性统计理论建立之前（1940年）提出了一种描述橡胶弹性的唯象理论。该理论有两条假定：

（1）橡胶是不可压缩的，在未应变状态下各向同性

（2）简单剪切形变的状态方程可由虎克定律描述

  基于这两个假定，Mooney从对称性出发，由纯粹的数学论证推导出橡胶材料的应变储能函数具有如下形式：

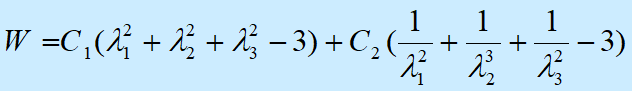
对非线性弹性是一个突破，它使我们不需作任何关于应力应变关系的假定而能得到非线性弹性的应力应变关系。当然这一理论比线弹性理论复杂得多。下面我们讨论的是一种特殊情况下的结果，即取W的级数展开式的头二项加以处理，我们称之为Mooney-Rivlin理论

5.2.4拉伸

根据Mooney-Rivlin理论：

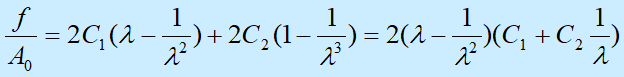
式中，C1和C2为常数，称为Mooney-Rivlin常数，它们表示材料的非线性弹性。式中应力采用工程应力。l为达到平衡时的拉伸比。如果e<<1，即应变很小，则

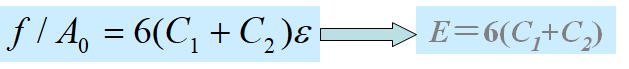
5.2.5简单剪切

在简单剪切中，Mooney-Rivlin理论的结果为

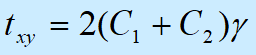
上式说明在简单剪切中txy与g也存在线性关系，但这里g可以很大，与线弹性比较，当g<<l时，

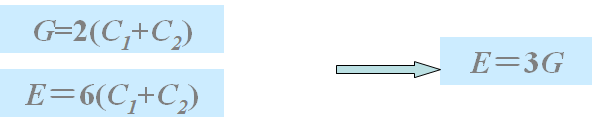
这并不是Mooney-Rivlin理论处理简单剪切的唯一结果，另一个结果与线弹性完全不同，即在橡胶弹性的剪切变形中，法向应力差不是0，而是

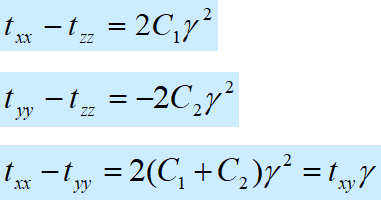
这与线弹性的结果完全不同。这说明，如果对一个橡胶物体作非线性的简单剪切试验，只施切向应力txy和txy是不够的，还必须在三个不同的法向施加法向应力，否则变形就不是简单剪切，在法向上也会发生变形。这种作用称为法向应力效应

5.2.6非线性弹性理论的适用范围 

只有部分交联的聚合物在高于Tg时才会发生较大的弹性形变（可恢复的变形）。当然交联不一定是指化学上的交联（如橡胶的硫化），也包括大分子间由于其他原因而紧密地结合在一起的情况。如嵌段共聚物在温度介于共聚物组成中两个聚合物的Tg之间时。

非线性弹性理论适用于橡胶材料，即部分交联的聚合物，其Tg低于室温。双组分体系，溶胀的聚合物即由交联的聚合物与其吸收的溶剂组成的体系也会产生较大的弹性变形。

Mooney-Rivlin理论的局限性是它仅适用于平衡的变形，即f或l必须是平衡态时的，不随时间变化