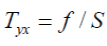2.2.1应力的分量表示法和应力张量

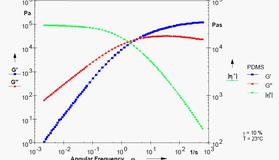
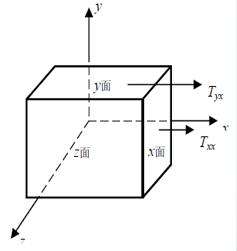
采用应力的分量表示法可完全地描述一个应力的性质：应力方向、大小、作用面。应力分量用两个下标表示。第一个表示该应力作用面，第二个表示应力方向。

作用力的方向与作用面垂直，被称为应力的法向分量（Normal component），即两个下标相同的分量为法向分量。

作用力的方向与作用面平行，这种分量被称为应力的切向分量（Shear component）

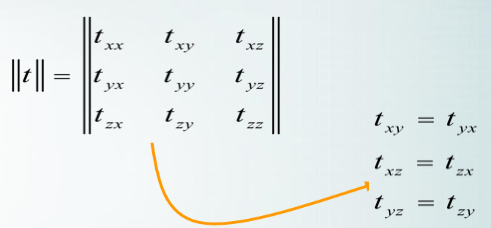
应力张量中只有六个是独立的，只要知道这六个应力分量，就能完全描述材料的受力状态。

2.2.2 简单实验中的应力张量

1、拉伸实验

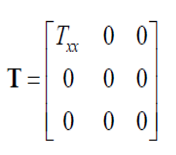
2、各向同性的压缩

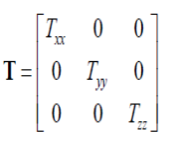在各向同性压缩实验中，应力在任何方向都与作用面垂直而且大小相同，即在笛卡尔坐标中： txx=tyy=tzz=p，其他切应力分量均为零。

3、简单剪切

2.2.3 接触力（内力）

  接触力是物体内的一部分通过假想的分隔面作用在相邻部分上的力，也即外力向物体内传递

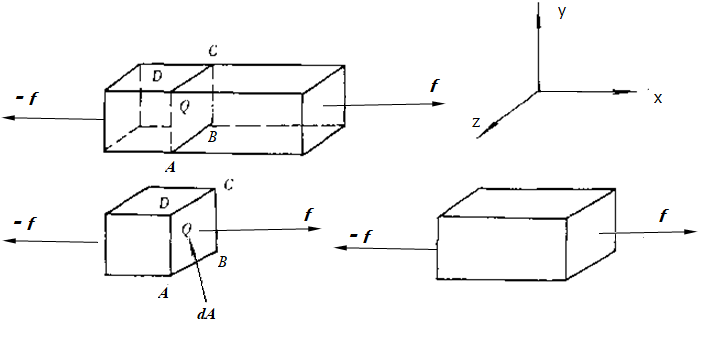
分隔面与x轴垂直 

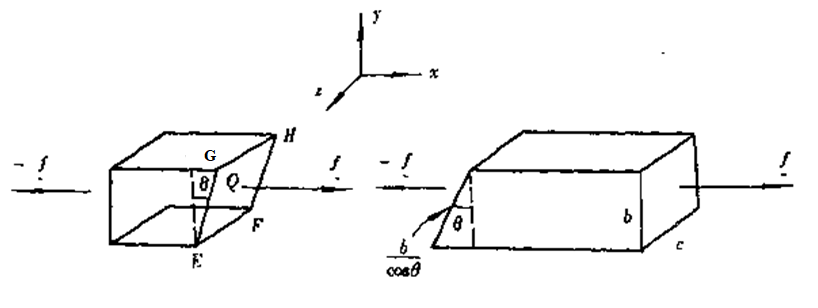
q面与x平面的面积不同,q面的面积为A/cosq

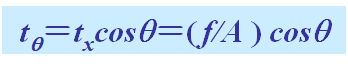
tq分解为：tq的法向分量；tq的剪切分量