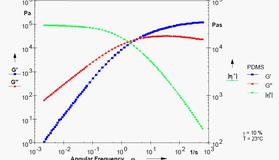
已学的四种模式，来描述高聚物在一定条件下表现出的性状：
线弹性:适用于在低于玻璃化温度下的高聚物
非线性弹性:适用于高于Tg时的部分交联的高聚物 或高弹态聚合物
线性及非线性粘性：适用于高聚物溶液及高聚物熔体
实质上，高聚物的性状并不能用以上四种简单模式来表示
高聚物在应力作用下，可能同时表现出弹性和粘性
高聚物在一般情况下，在恒定应力作用或一定应变下，表现出应变的时间依赖性或应力的时间依赖性Time- dependent
对一般情况下的高聚物，用粘弹性（Viscoelasticity）来表示
线性粘弹性 非线性粘弹性
粘弹性可以用测定形变的时间依赖性的实验来说明
应变史（Strain history）：应变是随时间而变化的，用e(t)表示它
应力史（Stresshistory）：应力是随时间而变化的，用s(t)表示它
7.1.1 蠕变实验
蠕变：
在不同的材料上瞬时地加上一个应力，然后保持恒定即
s(t)＝0 t≤0
s(t) ＝s0 t≥0
式中，s0中的下标表示应力是在时间为零时加上去的（下面我们将看到应力不是在时间为0时加上去的情况），然后观察各种材料的应变随时间的变化，这种实验称为蠕变。
各种材料有不同的响应，如图7.1所示
图7.1蠕变实验
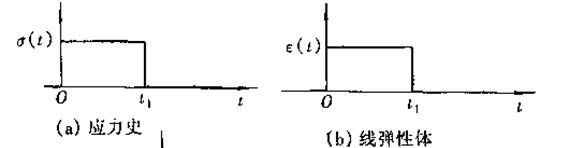
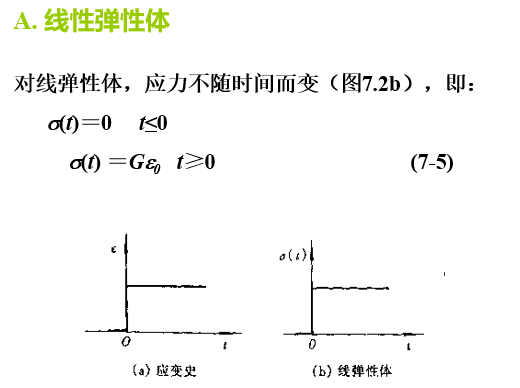
A. 线性弹性体
对线性弹性体，弹性应变是瞬时发生的，不随时间而变（图7.1b）。即
e(t)=0 t≤0
e(t)=Js0 t≥0 (7-1)
线弹性固体在除去应力时也能立刻恢复又原有形状（图7.1b）。弹性形变的特点之一是变形时能储藏能量，而当应力除去后，能量又释放出来使形变消失
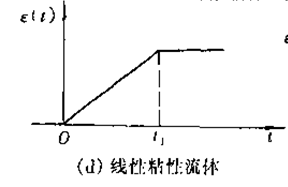
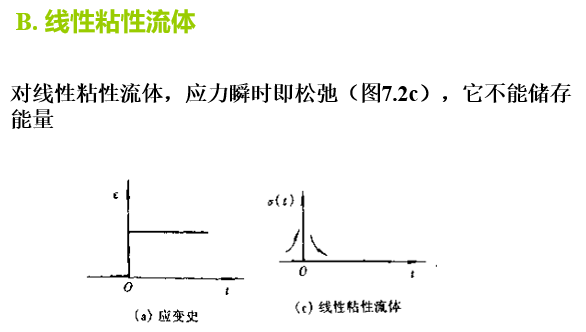
B. 线性粘性流体
对线性粘性流体，有（图7.1d）：
e(t)=0 t≤0
e(t)=s0t/h t≥0 (7-2)
线性粘性流体的应变是随时间以恒定的应变速度发展的，而除去应力后应变即保持不变，称之为发生了流动（图7.1d），即能量是完全散失的
 |  |
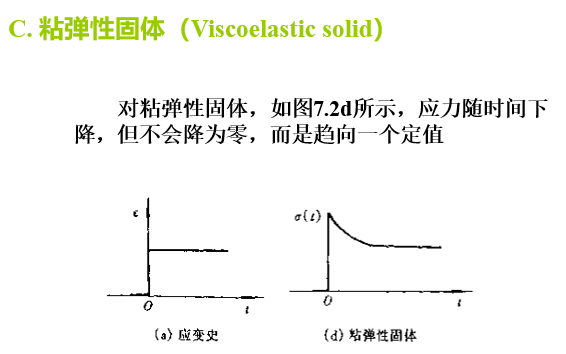
C. 粘弹性固体（Viscoelastic solid）
实际上，聚合物的响应是不同于以上两种理想模式的
v有的聚合物材料如部分交联的弹性体，表现出的性状如（图7.1c）所示，即应变随时间逐渐增大，但并不是无限地在发展，而趋向于一个定值，可称之为橡胶平台（Rubberplateau）。如果时间t1瞬时除去应力s0，可发现经过相当长的时间，该材料能完全恢复其原有的形状（图7.1c）
图7.1c所示的材料则既具有粘性，即应变随时间发展，又具有弹性，即应力除去后，应变逐渐减小，直至完全消失，即材料变形时没有发生粘性流动，所以称之为粘弹性固体（Viscoelastic solid）
 |  |
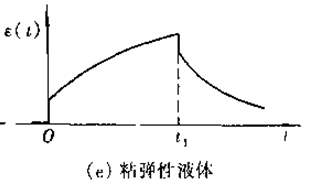
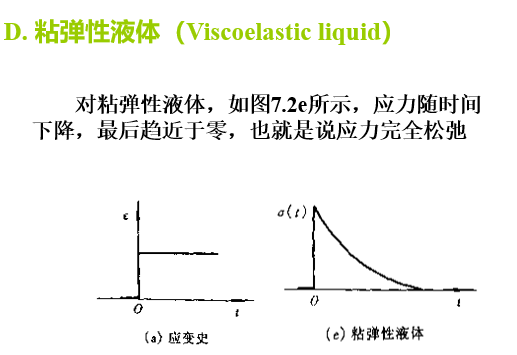
D. 粘弹性液体（Viscoelastic liquid）
形变是随时间发展的，而且不断发展，并趋向恒定的应变速度（与粘性流体类似）。这种材料在应力除去后，只能部分恢复，留下永久变形（图7.1e），即这种材料在蠕变时发生了粘性流动，所以称之为粘弹性液体（Viscoelasticliquid）
|  |
弹性常数
对线弹性体：用弹性常数J或D就可表示其弹性
对线性粘性流体：用粘度h表示其粘性
对粘弹性体，无论是粘弹性固体或是粘弹性液体，应变都是随时间变化的，因而弹性常数也是随时间而变的,在上述蠕变中：
了解整个时间谱范围内的J(t)。不同的粘弹性体有不同的J(t)。这反映了材料的微观结构的差异，因此粘弹性理论不仅有实践意义，而且能揭示聚合物的内部结构。
同样，由拉伸蠕变实验，我们有：
D(t)=e(t)/s0 (7-4)
7.1.2应力松弛（Stressrelaxation）实验
应力松弛：
使材料试样瞬时地产生一个应变，然后使它保持不变，即
e(t)=0 t≤0
e(t)=e0 t≥0
然后观察应力随时间的变化。这种实验称为应力松弛
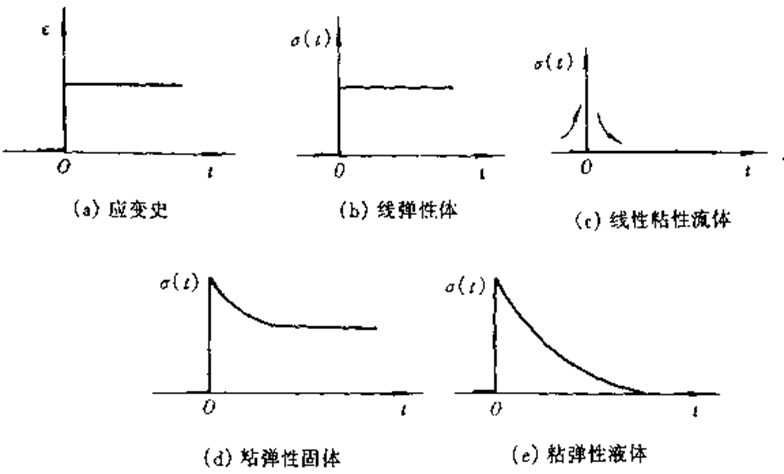
图7.2应力松弛实验
弹性常数
无论是粘弹性固体或是粘弹性液体，应力都是时间的函数、因此其模量G也是时间的函数：
s(t)＝0 t≤0
s(t)＝S(e0,t) t≥0 (7-6)
G(t)＝S(e0,t)/e0
对粘弹性体，要表征其性状，必须了解G(t)，它是材料的性质，是其内部结构的反映
同样，对拉伸应力松弛实验，有拉伸松弛模量：
E(t)＝S(e0,t)/e0 (7-7)
必须指出，我们用蠕变实验来定义柔量，用松弛实验来定义模量
即 J(t)≠1/ G(t)
必须记住，J(t)，D(t)只能从蠕变实验中测出，G(t)、E(t)只能从应力松弛实验中求出
