系统结构图(框图、方块图)模型可以直观而完整地表示受控变量与输入量之间的关系。但是，对于复杂关联关系的系统而言，框图的化简是一项琐碎甚至难以完成的任务。

描述系统变量之间关联关系的另一种方法是由梅逊(Mason)提出的，以节点间的线段为基本的描述手段。这种基于线段的方法就是信号流图法。优点在于：对流图进行化简和变换，就可以利用流图增益公式，方便地给出系统变量之间的信号传递关系。

信号流图由节点及连接节点的有向线段构成，是一组线性关系的图示化表示。

1.信号流图及其术语

信号流图由节点及连接节点的有向线段构成，是一组线性关系的图示化表示。

反馈理论关注的要点是系统中信号的变换和流向，因此信号流图特别适用于反馈控制系统。

信号流图的基本要素是连接彼此关联的节点的具有单一方向的线段，称为支路。

表示输入、输出信号的点称为节点，既有输入也有输出的节点称为混合节点。

表示从一个信号(节点)到另一个信号(节点)的，由一条或多条相连的支路构成的路径，称为通路。

表示从起始节点和终止节点为同一节点，且与其他节点最多相交一次的封闭通路，称为回路。

若两个回路没有公共节点，称为不接触回路。

(1)节点

(2)支路

(3)输入节点与输出节点

(4)混合节点

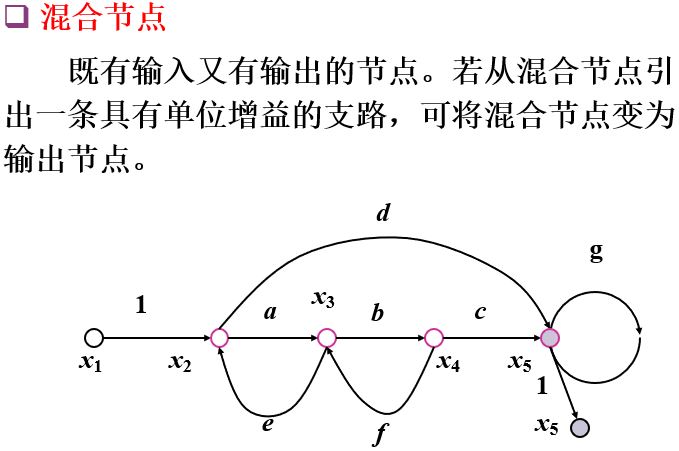
(5)通路

(6)回路

2.信号流图的绘制

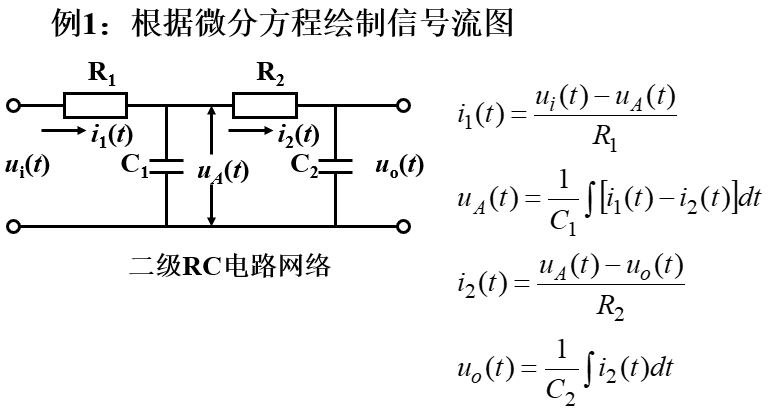
(1)由系统的微分方程绘制信号流图

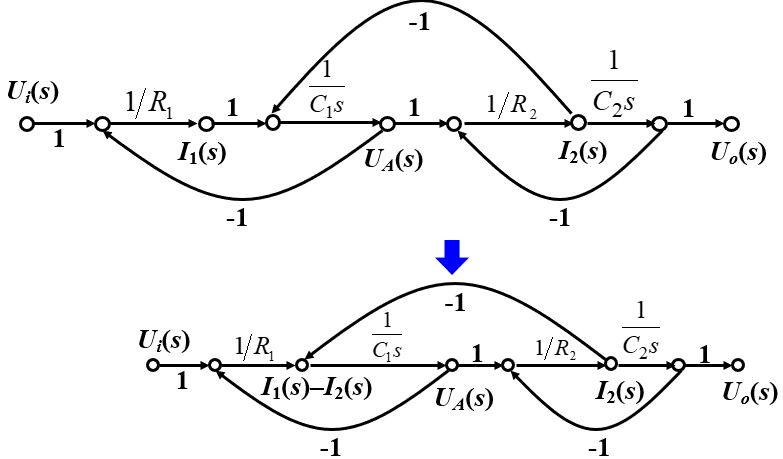
由系统的微分方程绘制信号流图时，应先进行拉氏变换，将微分方程变换为s的代数方程后再绘制信号流图。

绘制信号流图时，首先对系统的每个变量指定一个节点，并按照系统中变量的因果关系，从左往右顺序排列；再把代数方程中变量之间的关系作为支路增益，用支路将各节点变量准确连接，可得到系统的信号流图。

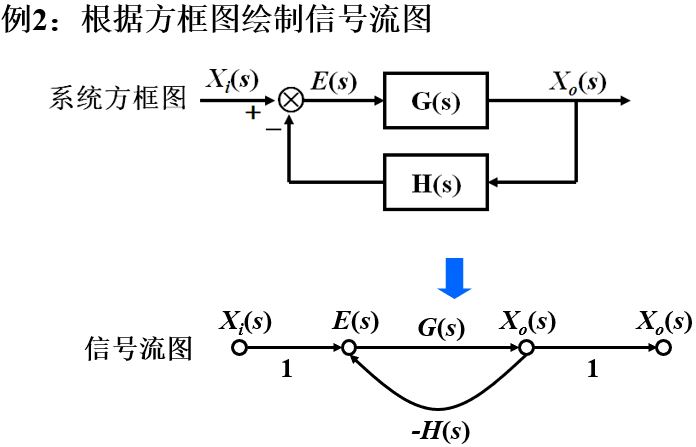
(2)由系统结构图(框图、方块图)绘制信号流图

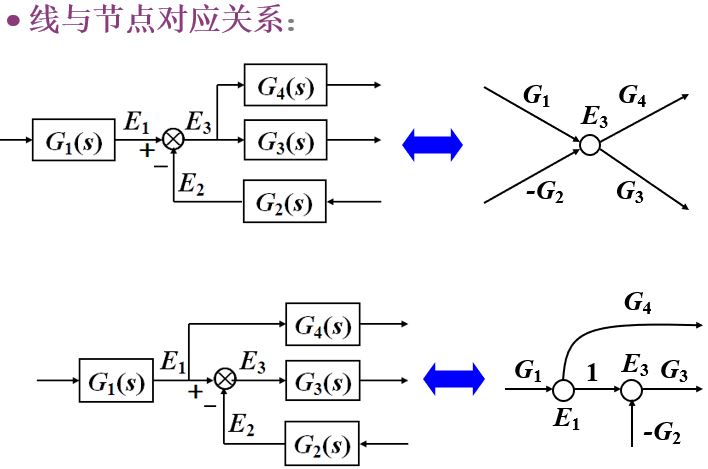
由系统结构图绘制信号流图时，结构图中的信号线、比较点和引出点都成为节点，方框成为支路，框中的传递函数成为相应支路的支路增益。于是结构图就变换成相应的信号流图。

注意：信号流图中节点的输出信号等于该节点诸信号的叠加，所以在由结构图转化为信号流图时，要注意引出点与比较点的画法，比较点之前的引出点必须单独设置节点。

3.梅逊增益公式

信号流图的输入节点(输入变量)到输出节点(输出变量)的系统传递函数，可直接用梅逊公式求取。

梅逊公式：

示例：

1.

2.

本节必看视频(与上节必看视频相同，本节内容包含在其中)：