通常用微分方程来描述包含自动控制环节的动态物理系统。

引入拉氏变换之后，求解微分方程简化为求解代数方程。

由于控制系统着眼于对特定变量的控制，因此，必须将控制变量和受控变量联系起来，并弄清楚它们之间的关系。

传递函数表示的正是输入变量和输出变量之间的这种关系。可见，传递函数时控制工程的一个重要分析工具。它也为表示系统变量之间相互关系的其他图示化模型提供了便利。

系统结构图模型(方块图)就是这样一种广泛应用于控制工程的图示化模型，是控制系统的动态数学模型的图解形式。

结构图由单向的功能方块组成，这些方块代表了变量的传递函数。

控制系统的框图包含四种基本单元：信号线、引出点(测量点)、比较点(或综合点)和方框(方块或环节)。系统框图可按照如下步骤进行绘制：

(1)考虑负载效应，建立系统各元部件的微分方程；

(2)对各微分方程进行拉氏变换，写出其传递函数并画出响应的环节单元和比较点单元；

(3)按系统中各变量的传递顺序，依次将各元件的框图连接起来；置系统的输入变量于左端，输出变量于右端，得到系统的框图(方块图)。

1.框图的基本单元

(1)信号线

(2)信号引出点(测量点)

(3)比较点(综合点)

(4)函数方块(环节)

任何系统都可以由信号线、函数方块、信号引出点及求和点组成的方框图表示。

2.示例

3.框图(方块图)简化

(1)串联

(2)并联

(3)反馈

4.主要的结构图(方块图)简化规则：

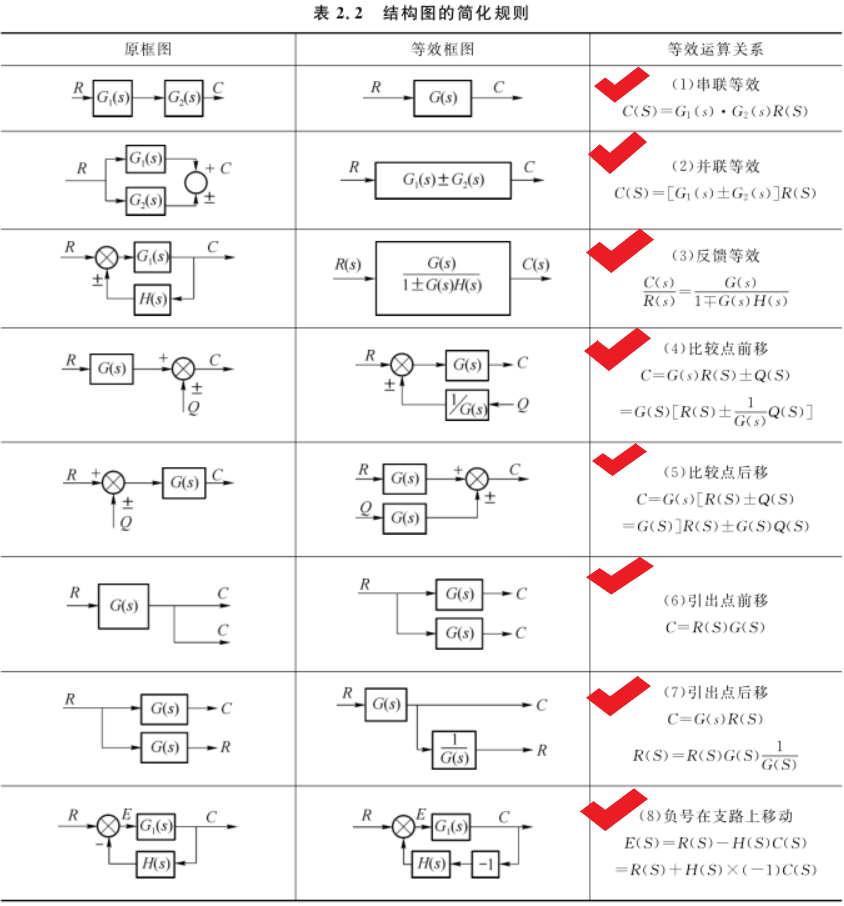
结构图中方块之间的基本连接方式有串联、并联、反馈三种。其相应的基本运算法则为：

(1)串联框图的等效传递函数等于各个方块传递函数的乘积；

(2)并联框图的等效传递函数等于各个方框传递函数的代数和；

(3)反馈连接的等效传递函数为

5.示例

求解系统的传递函数

本节必看视频(上一节必看视频包含本节部分内容，结合上一节必看视频学习)：

本节选看视频：