控制系统的微分方程,是时域中描述系统动态特性的数学模型,求解微分方程可以得到在给定外界作用及初始条件下系统的输出响应,并可通过响应曲线直观地反映出系统的动态过程。但系统的参数或结构形式有变化,微分方程及其解都会同时变化,不便于对系统进行分析与研究。
而根据求解微分方程的拉氏变换法,可以得到系统的另一种数学模型—传递函数。
1.传递函数的定义
线性系统的传递函数定义为:当两个变量的初值都假定为零时,即零初始条件下,输出变量的拉氏变换与输入量的拉氏变换之比。系统的传递函数表征了所研究的系统的动态性能。
传递函数的定义只适用于线性定常(系数为常数)系统。非定常系统,即时变系统中,至少有一个系统参数随时间变化,因为无法运用拉氏变换。传递函数只是系统的输入-输出描述,不提供系统内部结构和行为信息。有着相同形式的传递函数,可能对应着不同物理性质不同的系统,正如一些不同物理现象可以用相同形式的微分方程描述一样。

2.传递函数求解示例
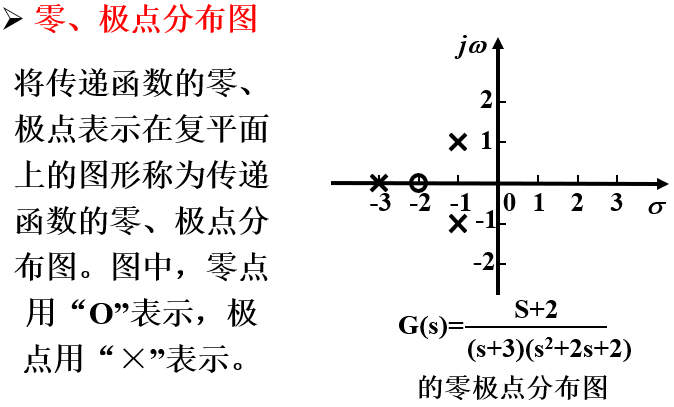
3.传递函数特征方程、零点和极点

4.脉冲响应函数
5.典型环节及其传递函数
环节:具有某种确定信息传递关系的元件、元件组或元件的一部分称为一个环节。经常遇到的环节称为典型环节。
任何复杂的系统总可归结为由一些典型环节所组成。
环节的分类:
(1)传递函数的“首1型”形式(零、极点形式)
(2)传递函数的“尾1型”形式(“典型环节”形式)
(3)从“首1型”到“尾1型”变换
(3)典型环节
除此以外,实际系统中还存在纯时间延迟现象,输出完全复现输入,但是有延迟,此时:
6.典型环节传递函数示例
(1)比例环节
(2)一阶惯性环节
(3)微分环节
(4)惯性微分环节
(5)一阶微分环节
(6)积分环节
(7)二阶振荡环节
(8)延迟环节
上述各典型环节,是从数学模型的角度来划分的。它们是系统传递函数的最基本构成因子。在和实际元件相联系时,应注意:
(1)系统的典型环节是按数学模型的共性来划分的,它与系统中使用的元件并非都是一一对应的,一个元件的数学模型可能是若干个典型环节的数学模型的组合。而若干个元件的数学模型的组合也可能就是一个典型数学模型;
(2)同一装置(元件),如果选取输入、输出量不同,它可以成为不同的典型环节。如直流电动机以电枢电压为输入、转速为输出时,它是一个二阶振荡环节,若以电枢电流为输入、转速为输出,它却是一个积分环节;
(3)在分析和设计系统时,将被控对象(或系统)的数学模型进行分解,就可以了解它是由哪些典型环节所组成的。因而,掌握典型环节的动态特性将有助于对系统动态特性的分析研究;
(4)典型环节的概念只适用于能够用线性定常数学模型描述的系统。
7.传递函数的主要性质
(1)传递函数的概念只适用于线性定常系统,它与线性常微分方程一一对应;
(2)传递函数的概念主要适用于单输入单输出系统。若系统有多个输入信号,在求传递函数时,除了一个有关的输入外,其他输入量一概视为零;
(3)传递函数时s的有理分式,对实际系统而言坟墓的阶次n大于分子的阶次m,此时称为n阶系统;
(4)传递函数仅与系统的结构和参数有关,与系统的输入无关;只反映了输入和输出之间的关系,不反映中间变量的关系;
(5)传递函数原则上不能反映系统在非零初始条件下的全部运动规律;
(6)一定的传递函数有一定的零、极点分布图与之对应。
本节必看视频:
必看课件PPT:
第二章选看短视频(第一部分):
第二章测验1:


