在参数变化的一定范围内，绝大多数的物理系统呈现出线性特性，不过，总体而言，当不限制参数的变化范围时，所有的物理系统终究都是非线性系统。

比如，质量-弹簧-阻尼系统中，当质量块的位移较小时，可以采用线性微分方程描述其为线性系统，但是当位移不断增大时，弹簧最终将会因为过载而变形断裂。因此，需要仔细研究每个系统的线性特性和相应的线性工作范围。

1.线性系统与非线性系统

线性系统：

非线性系统：

2.系统数学模型线性化方法

非线性方程难于求解，用线性数学模型近似表示非线性数学模型。

在一定工作范围内进行线性化处理。

将非线性函数在平衡点附近展开成泰勒级数，并忽略高次项。

例：直流发电机

X轴表示励磁电流，Y轴表示输出电势。由于存在磁路饱和，y和x呈非线性关系y=f(x)，可以在(x0,y0)附近泰勒级数。

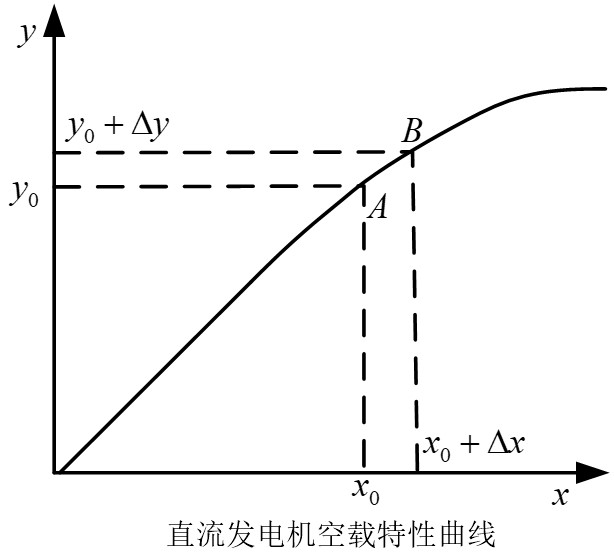
忽略高次项，然后用增量表示：

经上述处理后，就成为线性方程。这就是非线性系统的线性化模型，称为增量方程。

增量方程的数学含义就是将参考坐标的原点移到系统或元件的平衡工作点上，对于实际系统 ，就是以正常工作状态为研究系统运动的起始点，这时，系统所有的初始条件均为零。

由于反馈系统不允许出现大的偏差，因此，这种线性化方法对于闭环控制系统具有实际意义。

对于具有两个自变量的非线性函数y=f(x1,x2),在静态工作点y0=(x10,x20)附近展开成泰勒级数。

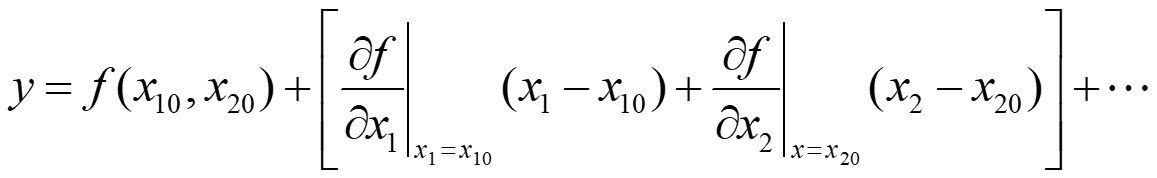
用增量表示

上述方法称为小偏差线性化方法。这是基于这样一种假设：输入量和输出量只是在静态工作点附近作微小变化。对于某些眼中的典型非线性，如继电特性、间隙以及摩擦等，不能进行求导运算，所以只能作为非线性问题来处理。

实例：

3.线性化注意事项

(1)线性化是针对某一额定工作点的，工作点不同，则所得方程系数也往往不同；

(2)增量越小，精度越高。当增量(工作范围)较大时，为了验证容许的误差值，需要分析泰勒级数中的余项；

(3)线性化只适用于非本质非线性系统。即在额定工作点周围的工作范围内没有间断点、折断点的单值函数。

本节必看视频(视频最后部分涉及下一节部分内容，请注意)：