一、力的功—一、力的功

—定义：力对质点所作的功等于力在质点位移方向的分量与位移大小的乘积。

设质点M在任意变力F作用下沿曲线运动，在一个无限小位移中力作的功称为元功δW。

元功：δW=Fcosθds 或δW=F·dr  单位：J(焦耳)

力在全程作的功：

在直角坐标系：F=F_xi+F_yj+F_zk，dr=dxi+dyj+dzk

二、常见力所作的功

1、重力的功

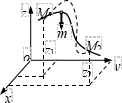
设质点由M₁运动到M₂。

重力P=mg在直角坐标轴上的投影为：F_x=0，F_y=0，F_z= -mg

重力作功：

可见重力作功仅与质点运动的始、末位置的高度差有关，

与运动轨迹的形状无关。

对质点系：W₁₂=∑m_ig(z_i1-z_i2)

∵mz_c=∑m_i z_i，∴W₁₂= mg(z_c1-z_c2)

质心下降，重力作正功；质心上移，重力作负功。

2、弹性力的功

可见，弹性力作功只与弹簧在始末位置的变形量δ有关，当δ1>δ2时，弹性力作正功，当δ1<δ2时，弹性力作负功。

3、定轴转动刚体上作用力的功
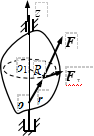