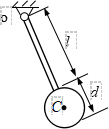
1、质点的动量矩

与力对点之矩相似

M_O(mv)=r×mv  质点的动量对点O的矩

[M_O(mv)]_z=M_z(mv) 质点对点O的动量矩矢在某轴上的投影，等于质点对该轴的动量矩。

2、质点系的动量矩

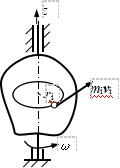
L_O=∑M_O(m_iv_i)    质点的动量对点O的矩

L_z=∑M_z(m_iv_i)      质点系的动量对z轴的矩

[L_O]_z=L_z    质点系对点O的动量矩矢在某轴上的投影，等于质点系对该轴的动量矩

刚体平移时：可将质量集中于质心，作为一个质点计算其动量矩。

定轴转动刚体：

L_z=∑M_z(m_iv_i)=∑m_iv_ir_i=∑m_i(ωr_i)r_i=ω∑m_i r_i²

令：J_z=∑m_i r_i²——刚体对z轴的转动惯量，则：L_z= J_zω

3、刚体对轴的转动惯量

1、简单形状物体的转动惯量                                                             

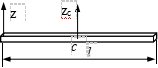
(1)均质细直杆对z_c轴的转动惯量  设质量为m，杆长l 

J_z=∑m_i r_i²=

(2)均质薄圆环(薄壁圆筒)对中心轴的转动惯量  

J_z=∑m_i r_i²=R²∑m_i=mR²

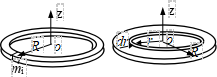
(3)均质圆板(圆柱)对中心轴的转动惯量

J_z=∑m_i r_i²=

2、惯性半径

令——惯性半径或回转半径，则：

对简单几何形状或几何形状已标准化的零件的惯性半径、转动惯量可在有关手册中查到，书272-273页。

3、平行轴定理

定理：刚体对于任一轴的转动惯量，等于刚体对于通过质心、并与该轴平行的轴的转动惯量，加上刚体的质量与两轴间距离平方的乘积。即：J_z=J_zc+md²    证明见书269页

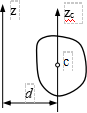
例11.1 质量为m，长为l的均质细杆，求J_z

_{解：Jz=Jzc+m(l/2)²=ml²/12+ ml²/4= ml²/3}

例11.2 钟摆简化如图，均质细杆质量m₁，杆长l，均质圆盘质量m₂，圆盘直径为d。求摆对悬挂点O的水平轴的转动惯量。

解：J_o=J_o杆+ J_o盘  ，J_o杆= m₁l²/3

J_o盘=J_盘c+ m₂(l+d/2)² 

⁼