§8.1 刚体平面运动的概述和运动分解
一、平面运动
在运动中,刚体上的任意一点与某一固定平面始终保持相等的距离。
平面运动刚体上的各点都在平行于某一固定平面的平面内运动。
例:沿直线轨道滚动的车轮,平面曲柄连杆机构中AB的运动,平面四杆机构中连杆AB的运动。

二、刚体平面运动的简化

如上图一作平面运动的刚体,用一平行于固定面的平面截割刚体得一平面图形,该平面图形内任一点始终在该平面内运动。过图形上任一点作垂直于图形的直线,则当刚体作平面运动时,该直线作平移。因此,平面图形上的点与直线上各点的运动相同。因此平面图形上各点的运动可以代表刚体内所有点的运动。
刚体的平面运动可简化为平面图形S在其自身平面内的运动。
三、平面运动的分解
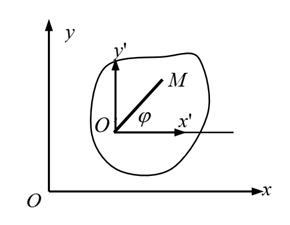
平面图形在其平面上的位置完全可由图形内任意线段的位置来确定,而要确定此线段在平面内的位置,只需确定线段上任意一点的位置及线段与x轴夹角即可。
1、平面图形的运动方程:
xo’=f1(t ),yo'= f2(t ),j= f3(t )
2、平面运动的分解
运动方程分两部分:一部分是按O’点运动方程的平移,没有转动;另一部分是绕O’点的转动。
基点—平面图形上任取一点O’,其上安上平移参考系o’x’y’,一般o’x’y’与定坐标系oxy各轴平行。
平面图形的平面运动可看成为随基点的平移和绕基点转动这两部分运动的合成。
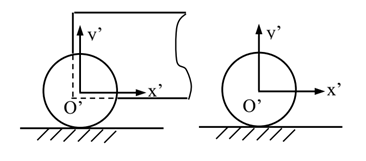
例沿直线轨道滚动的车轮:(见上图)
可取车厢为动参考体,以轮心为原点建立动参考系。 车轮的平面运动=车厢的平移+车轮绕O’的转动,单独的轮子作平面运动时,可在轮心固连平移参考系,同样可把轮子的平面运动分解为平移和转动的合成。
3、基点选择不同,对运动分解的影响

图中连杆AB作平面运动,可取点A或B为基点,点A作圆周运动,点B作水平直线运动,因此,平面图形上基点选择不同,其动参考系的平移是不同的,其速度和加速度是不相同的。
由图,AB连线绕A点和绕B点的转角,任一时刻相同,因此其角速度、角加速度也必然相同。
结论:平面运动可取任意基点分解为平移和转动,其中平移的速度和加速度与基点的选择有关,而平面图形绕基点转动的角速度和角加速度与基点的选择无关。


