§7-1 相对运动·牵连运动·绝对运动

一、运动的合成与分解

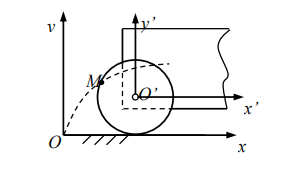
       点M相对地面的旋轮线运动(分解)→ ←(合成)点M相对车厢的圆周运动+车厢相对地面的平移

二、基本概念

两个参考系：定参考系oxy—一般固连于地面

动参考系o’x’y’—固连在相对地球运动的参考体上

三种运动：绝对运动—动点相对定系的运动

                 相对运动—动点相对动系的运动

                 牵连运动—动系相对定系的运动

三种速度、加速度：

绝对：速度va；加速度aa，相对：速度vr；加速度ar，牵连：速度 ve；加速度ae

牵连速度和牵连加速度是指动系上与动点重合的那一点的速度和加速度。

例 7.1 已知 AB 杆的ω、α，试分析点 M 的三种运动、速度、加速度。

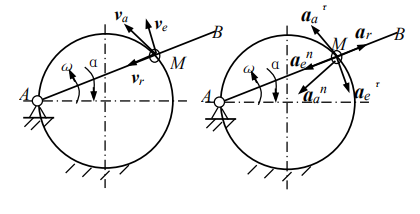
解：1、动点—小圆环 M定系—固连于地面动系—固连于 AB 杆

       2、运动分析绝对运动—M 沿大圆环的圆周运动相对运动—M 沿 AB 杆的直线运动牵连运动—杆 AB 绕 A 点的转动

      3、速度：va、vr、ve 如图

      4、加速度如图。

三、运动方程和轨迹动

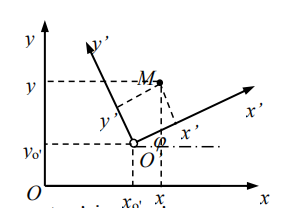
点—M，定系—oxy，动系—o’x’y’

绝对运动方程：x=x(t)，y=y(t)，消去 t 得绝对运动轨迹相对运动方程：x’=x’(t)，y’=y’(t)，消去 t 得相对运动轨迹

牵连运动方程(动系相对定系)：

三者间的关系：

例 7.2 车削工件端面，oxy 为定系，工件以等角速度ω转动，刀尖 M 沿 x 轴往复运动，运动方程为 x=bsinωt。求车刀在工件端面上切出的痕迹。

解：动点—M，动系 o’x’y’—固定在工件上由图：x’=xcosωt，y’= -xsinωt ∵x=bsinωt ∴x’= bsinωt cosωt=(b/2) sin2ωty’= - bsinωt sinωt= -(b/2)(1-cos2ωt)上式中消去时间 t 得刀尖的相对轨迹方程：(x’)2+(y’+b/2)2=b2/4——车刀在工件端面上切出的痕迹是一个半径为 b/2，圆心在 Oy’轴上，圆周过工件中心 O。