§3-1 空间汇交力系

一、力在直角坐标轴上的投影

投影：Fx=Fcos(F，i)=Fsinγcosφ

          Fy=Fcos(F，j)=Fsinγsinφ

          Fz=Fcos(F，k)= Fcosγ

当力F与坐标轴x、y间的夹角不易确定时，可先把力F投影到Oxy平面，得到力Fxy，再进一步投影到x、y轴。

二、空间汇交力系的合成与平衡条件

1、合成：空间汇交力系的合力等于各分力的矢量和，合力的作用线过汇交点。

      FR=∑Fi

      FR=∑Fxi+∑Fyj+∑Fzk

      合力FR的大小和方向余弦：

      cos(FR，i)=∑Fx/FR，cos(FR，j)=∑Fy/FR，cos(FR，k)=∑Fz/FR

2、平衡的充要条件：合力 FR=0

  平衡方程：∑Fx=0，∑Fy=0，∑Fz=0

例3.1用起重杆吊起重物，起重杆的A端用球铰固定在地面上，B端用绳CB、DB拉住，两绳分别系在墙上的点C和D，连线CD平行于x轴，α=30°，CDB平面与水平面间的夹角∠EBF=30°，P=10kN。如起重杆的自重不计，求起重杆所受的压力和绳子的拉力。

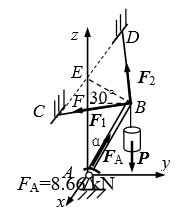
解：1、取起重杆AB和重物研究，受力如图。

2、列平衡方程。

∑Fx=0，F1cos45°-F2cos45°=0

∑Fy=0，FAsin30°-F1cos45°cos30°-F2cos45°cos30°=0

∑Fz=0，FAcos30°+F1cos45°sin30°+F2cos45°sin30°-P=0

3、解方程得：

F1=F2=3.54 kN

FA=8.66kN