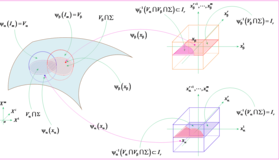
课程架构

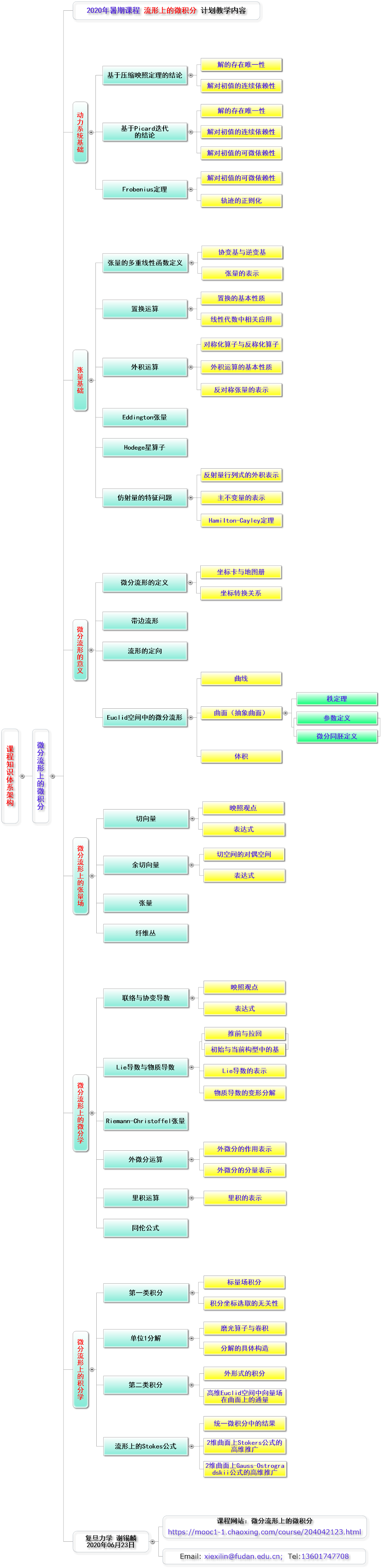
教学计划

教与学的内容按知识内容进行安排，现具体包含12部分。

每部分包括：（1）第一阶段 基于在线资源的自学；（2）第二阶段 固定时间的讲述与研讨，包括教师讲述内容，师生研讨内容；（3）第一阶段自学教学视频目录，在开始第二阶段前务必完成这部分视频的自学。

每部分一般对应1周的教与学，个别对应2周的教与学；总计对应16周的教与学。

 

§01 Euclid空间中微分同胚的相关结论（1周教与学）

§第一阶段基于在线资源的自学

1.   秩定理 ① 内容。② 分析过程。

2.   Morse定理 ① 内容。② 分析过程。

3.   Frobenius定理 ① 内容。② 分析过程。

§第二阶段 固定时间的讲述与研讨

1.    讲述：Euclid空间中微分同胚的相关结论 ① 秩定理。 ② Morse定理。③ Frobenious定理。

2.    研讨：① 上述三个定理的分析思想与主要技术。 ② 秩定理的相关应用。③ Morse定理的相关应用。④ Frobenious定理的相关应用

§第一阶段自学教学视频目录

1.    图示化讲述视频：① 秩定理。 ② Morse定理。③ Frobenious定理。

§02 张量的代数运算（1周教与学）

§第一阶段基于在线资源的自学

1.   局部协变基与逆变基秩定理① 协变基与逆变基的定义。② 基向量转换关系与分量转换关系。

2.   张量的定义与Morse定理 ① 按多重线性映照定义张量。② 3简单张量与张量的表示。

3.   张量的基本代数运算 ① 张量并。② e-点积与全点积。

4.   置换运算 ① 置换运算的定义与基本运算。② 置换算子的基本性质。

5.   置换算子① 置换算子的表述与复合。 ② 对称化算子。③反称化算子。

6.   外积运算① 外积的定义。 ② 外积的基本性质

7.   反对称张量① 反对称张量的定义。 ② 反对称张量的表示

§第二阶段 固定时间的讲述与研讨

1.    讲述：置换运算的基本性质

2.    讲述：置换算子的基本性质

3.    讲述：外积运算的基本性质

4.    研讨：① 上述三个定理的分析思想与主要技术。 ② 秩定理的相关应用。③ Morse定理的相关应用。④ Frobenious定理的相关应用

§第一阶段自学教学视频目录

1.    基于实体板书的讲述-2019年：① 置换运算。 ② 置换算子。③ 对称与反对称张量。④ 反称化算子的基本性质。⑤ 外积运算的基本性质。⑥ 反对称张量的表示。

§03 仿射量的特征问题（1+1周教与学）

§第一阶段基于在线资源的自学

1.   行列式的置换定义 ① 三种定义的等价性。② 基于行列式的置换定义获得行列式的基本性质。

2.   仿射量的行列式 ① 外积定义形式。② 两个结果形式。

3.   仿射量的主不变量 ① 外积定义形式。② 两个结果形式。

4.   仿射量的Cayley-Hamilton定理 ① 基于运算形式获得结论。② 相关应用。

§第二阶段 固定时间的讲述与研讨

1.    讲述：仿射量的行列式

2.    讲述：仿射量的主不变量

3.    讲述：仿射量的Cayley-Hamilton定理

4.    研讨：① 基于行列式置换定义获得行列式的基本性质。 ②仿射量主不变量的具体表示。③ 仿射量Cayley-Hamilton定理的相关应用。

§第一阶段自学教学视频目录

1.    基于实体板书的讲述-2019年：① 行列式的外积定义。 ② 主不变量的外积表示。③ Cayley-Hamilton定理。

§04 Eddington张量与Hodge-星算子（1周教与学）

§第一阶段基于在线资源的自学

1.   Eddington张量 ① 定义。② 基本性质。

2.   Hodge-星算子 ① 定义。② 基本性质。

§第二阶段 固定时间的讲述与研讨

1.    讲述：Eddington张量

2.    讲述：Hodge-星算子

3.    研讨：① Eddington张量的应用。② Hodge-星算子的应用，确定法向量，与叉乘的关系。

§第一阶段自学教学视频目录

1.    基于实体板书的讲述-2019年：① Eddington张量。 ② Hodge-星算子。

 

§05 欧氏空间中的体积流形与曲面流形（1+1周教与学）

§第一阶段基于在线资源的自学

1.   研究基础 ① 因果分解。② 微分同胚。

2.   体积流形 ① 内部坐标卡。② 边界坐标卡。

3.   曲面流形 ① 内部坐标卡。② 边界坐标卡。

§第二阶段 固定时间的讲述与研讨

1.    讲述：欧式空间中的体积流形

2.    讲述：欧式空间中的曲面流形

3.    研讨：① 流形定向的具体事例。 ② 体积流形坐标卡的具体实现。③曲面流形坐标卡的具体实现

§第一阶段自学教学视频目录

基于实体板书的讲述-2019年：① 基本知识回顾。 ② 流形内部坐标卡。③ 流形内部的坐标卡。④ 流形的定向。⑤ 诱导边界流形。⑥ 坐标卡的微分同胚与参数观点。

 

§06 切向量 余切向量 张量（1周教与学）

§第一阶段基于在线资源的自学

1.   切向量 ① 算子定义与其表示。② 基向量与分量的坐标转换关系。

2.   余切向量 ① 算子定义与其表示。② 基向量与分量的坐标转换关系。

3.   张量 ① 基于多重线性映照的定义。② 基向量与分量的坐标转换关系。

§第二阶段 固定时间的讲述与研讨

1.    讲述：切向量的算子定义与其表示

2.    讲述：余切向量的算子定义与其表示

3.    讲述：张量的多重线性映照定义与其表示

4.    研讨：① 切向量与余切向量的具体事例。 ② 张量的具体事例，结合力学、物理学等背景。

§第一阶段自学教学视频目录

基于电子板书的讲述：① 切向量。 ② 余切向量。③ 张量

 

§07 里积与外微分运算（1周教与学）

§第一阶段基于在线资源的自学

1.   里积运算 ① 定义。② 作用形式。③ 运算性质。

2.   外微分运算 ① 定义。② 作用形式。③ 运算性质。

§第二阶段 固定时间的讲述与研讨

1.    讲述：里积运算

2.    讲述：外微分运算

3.    研讨：① 里积运算的应用。 ② 外微分运算的事例。

§第一阶段自学教学视频目录

1.    基于实体板书的讲述-里积-2019年：① 里积的定义与基本性质。 ② 里积的作用形式。

2.    基于实体板书的讲述-里积-2019年：① 外微分的定义与Poincare性。 ② 反导性。③ 外微分与拉回或者推前的可交换性。④ 外微分与里积的可交换性。

§08 Lie导数（1周教与学）

§第一阶段基于在线资源的自学

1.   Lie导数的意义 ① 随体基。② 两种极限定义。

2.   Lie导数的极限分析 ① 极限分析方法。② 极限分析结论。

3.   Lie导数的基本运算性质 ① 切向量场的Lie导数。② 余切向量场的Lie导数。③ 张量场的Lie导数

4.   Lie导数的基本代数结构 ①Possion括号。

5.   Lie导数的作用形式 ① 整体作用形式。② 分量作用形式。

6.   同伦公式

§第二阶段 固定时间的讲述与研讨

1.    讲述：Lie导数的极限定义与分析

2.    讲述：Lie导数的运算性质，包括同伦公式

3.    讲述：Lie导数的作用形式

4.    研讨：① Lie导数不同极限定义的分析与结果。② Lie导数与物质导数之间的关系。

§第一阶段自学教学视频目录

1.    基于实体板书的讲述-里积-2019年：① Lie导数的意义。 ② Lie导数的极限分析。③Lie导数补的意义与极限分析。④ 张量场Lie导数的意义与结果。⑤ 向量场Lie导数的Possion括号。⑥ Lie导数的作用形式。

 

§09 联络（1+1周教与学）

§第一阶段基于在线资源的自学

1.   纤维丛 ① 切向量丛。② 余切向量丛。③ 张量丛。

2.   线性联络 ① 算子定义。② 曲率张量。③ 挠张量。

3.   切向量场的联络 ① 算子定义。② 表达形式。

4.   余切向量场的联络 ① 算子定义。② 表达形式。

5.   张量场的联络 ① 算子定义。② 曲率张量。③ 挠张量。

§第二阶段 固定时间的讲述与研讨

1.    讲述：纤维丛的流形定义

2.    讲述：线性联络

3.    讲述：切向量场、余切向量场、张量场的联络

4.    讲述：Cartan结构方程 ① 曲率方程。② 挠率方程。

5.    研讨：① 联络的具体实现，曲线、曲面、体积上张量场的联络。② 联络的事例。

§第一阶段自学教学视频目录

1.    基于实体板书的讲述-2019年：① 高维Euclid空间中的曲面。 ② 切向量场的联络。③ 余切向量场的联络。④ 张量场的联络

§10 正则子流形与其上联络（1+1周教与学）

§第一阶段基于在线资源的自学

1.   背景与研究基础 ① 微分同胚。

2.   正则子流形的坐标卡 ① 定义。② 坐标卡的构造。

3.   正则子流形上的联络 ① 底流形上的联络。② 子流形上的联络。

4.   典型事例 ① 低1维正则子流形。② 低r维正则子流形。

§第二阶段 固定时间的讲述与研讨

1.    讲述：正则子流形的定义与坐标卡

2.    讲述：正则子流形上的联络

3.    讲述：正则子流形的经典事例

4.    研讨：① 正则子流形的具体事例，m维Euclid空间中的曲面与抽象曲面。 ② 正则子流形的实际应用，联系与曲线与曲面上的场论。

§第一阶段自学教学视频目录

1.    基于图示化的讲述：① 背景与研究基础。 ② 正则子流形的坐标卡。③正则子流形上的联络。④ 低1维正则子流形。⑤ 低r维正则子流形

 

§11 微分流形上的积分（1周教与学）

§第一阶段基于在线资源的自学

1.   相关基础 ① Eddington张量。② Hodge-星算子。

2.   积分的定义 ① 第一类积分。② 第二类积分。

§第二阶段 固定时间的讲述与研讨

1.    讲述：Eddington张量与Hodge-星算子

2.    讲述：第一类与第二类积分

3.    研讨：① 现有积分定义与微积分中定义之间的关系。 ②流形上积分的事例。

§第一阶段自学教学视频目录

1.    基于实体板书的讲述-2019年：① 第一类积分。 ② 第二类积分。

 §12 微分流形上的Stoks公式（1周教与学）

§第一阶段基于在线资源的自学

1.   流形上Stokes公式的一般形式 ① 定理的结论。② 分析过程。

2.   流形上Stokes公式的旋度形式 ① 定理的结论。② 分析过程。

§第二阶段 固定时间的讲述与研讨

1.    讲述：流形上Stokes公式的一般形式

2.    讲述：流形上Stokes公式的旋度形式

3.    研讨：① 现有Stokes公式与微积分中相关结论之间的关系。② 流形上Stokes公式的应用事例。

§第一阶段自学教学视频目录

1.    基于实体板书的讲述-2019年：① 基本理论。 ② 应用事例。

本课程教学大纲（细致教学计划）