教学方式：递进性教与学 融合混合教学

本课程遵照递进性教与学的方式，融合混合教学的形式。整个教与学的阶段分为三个阶段：

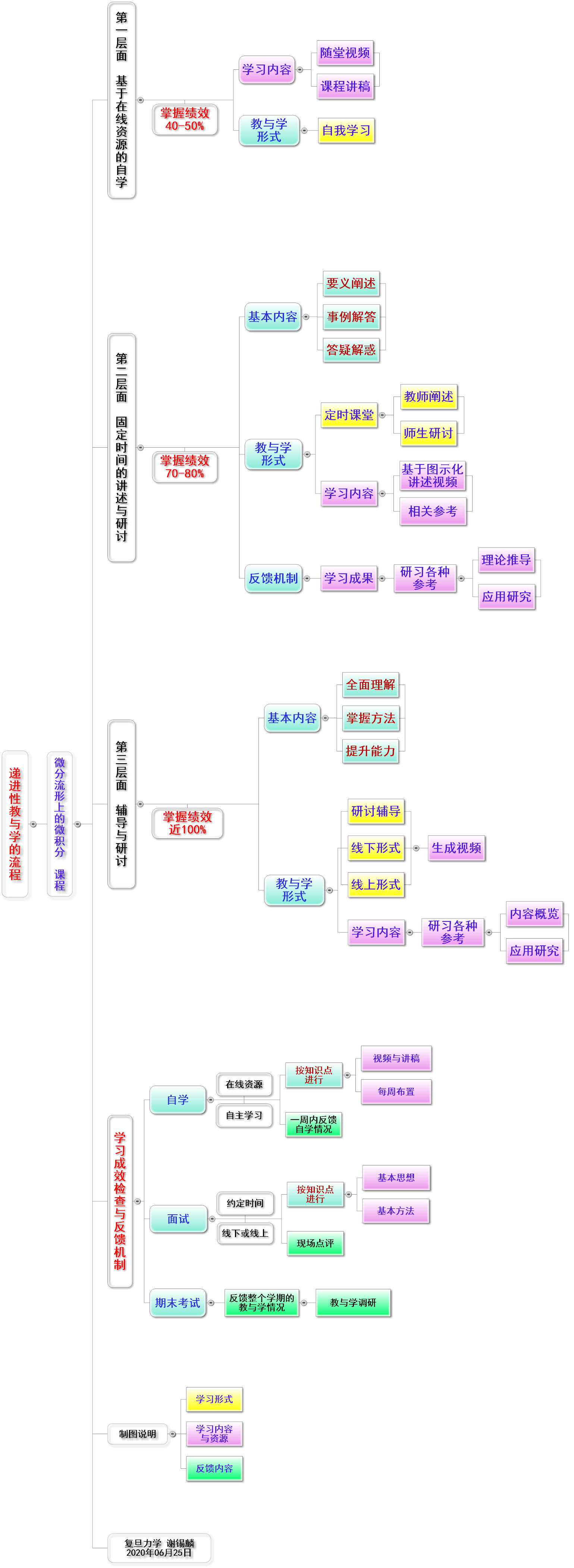
（1）第一阶段，基于在线资源进行自学。本课程提供周学习计划，同学们在课前完成相关教学视频与讲稿的学习，期待对思想与方法能有40-50%的掌握程度。

（2）第二阶段，固定时间的教师讲述与讨论。基于第一阶段的学习，本阶段的教师阐述注重知识的方法化、思想化、通识化，可以基于实体板书或者电子板书进行讲述；本阶段也将组织同学们进行相关内容的阐述，师生一起进行点评与讨论。通过本阶段的内容澄清与答疑解惑，期待对知识的掌握程度能提升至70-80%。

（3）第三阶段，辅导与研讨环节，包含约定时间的见面讨论，基于课程群的随时讨论。通过本阶段，期待同学们能全面理解与掌握思想与方法。本课程在开始前，我们会建立课程钉钉群，一般在钉钉群里进行相关通知、学习督促与自由讨论等。

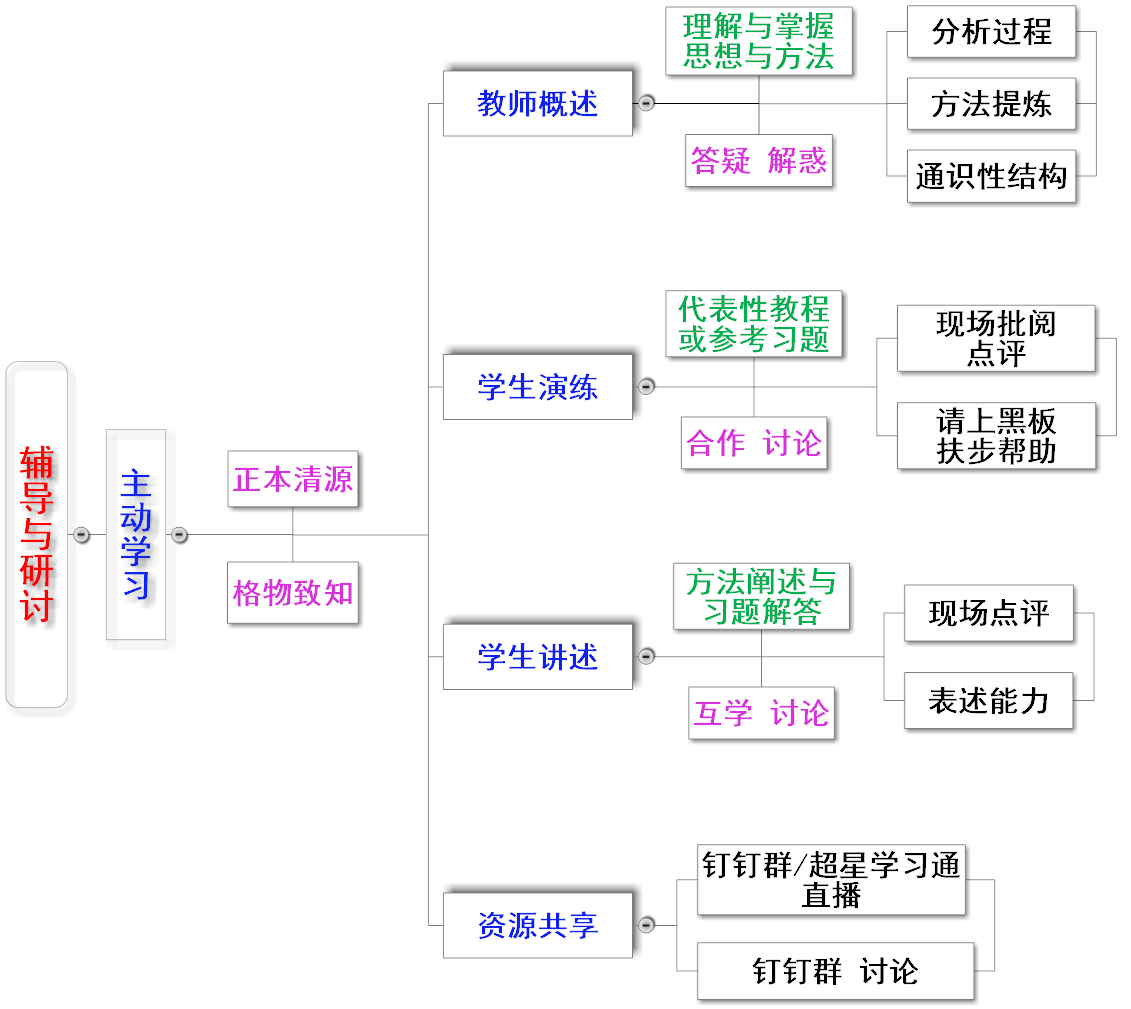
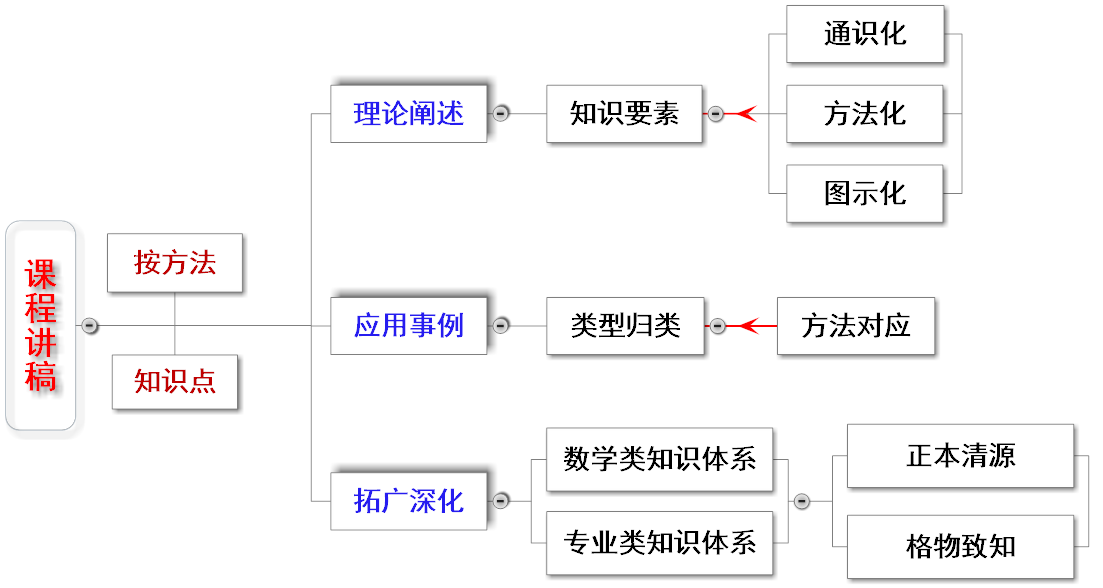
本课程就辅导与研讨环节的内容设计，如上图所示。按周计划的研讨内容，在教学计划中有说明，或者按教师实际的通知。

学习成效的自我检测

本课程注重基本理论（思想与方法）的学习，对于各部分内容的理解与掌握程度的自我检测，可以主要基于以下方面：（1）基于知识的图示化研究（本课程对应有基于图示化阐述的视频），经过学习能够自我阐述相关内容；（2）相关教程的课后习题（课程开展时，按进度会进行布置）；（3）历年本课程的考试试卷，可作为参考（位于本在线课程最后一章）。

在线资源

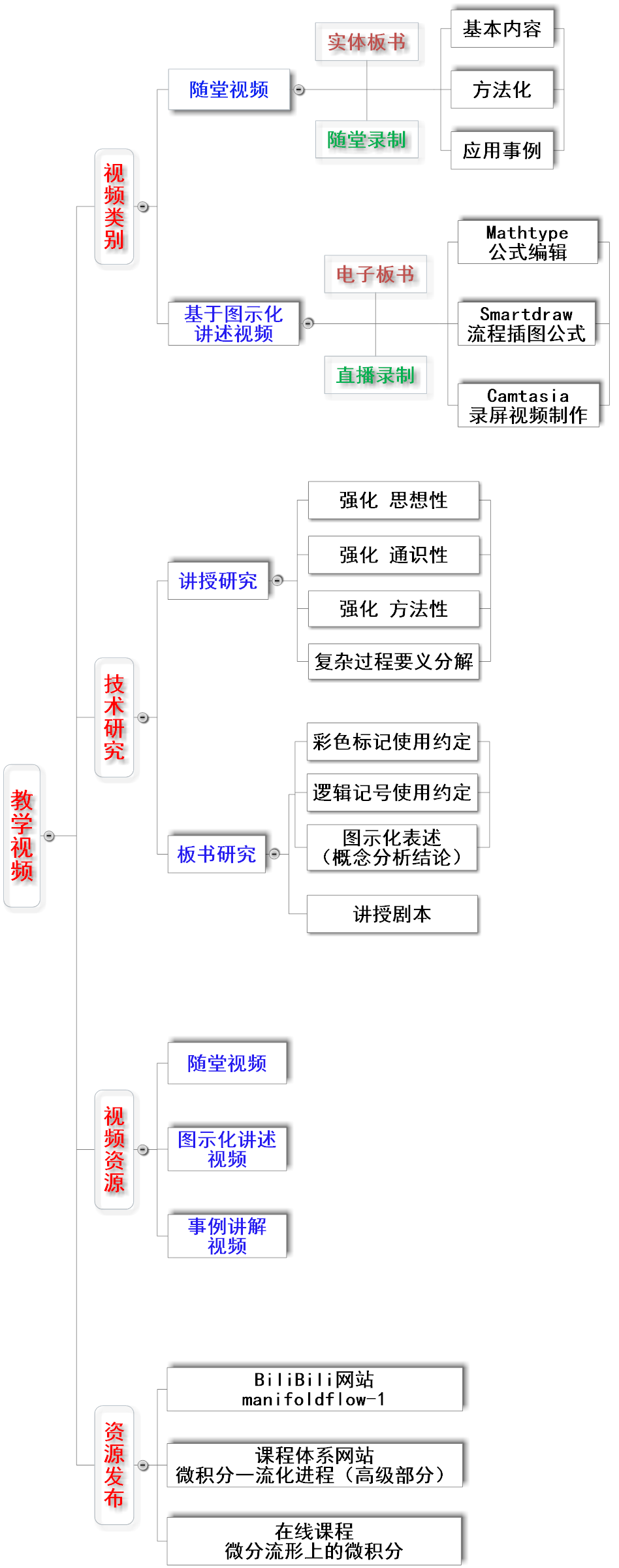
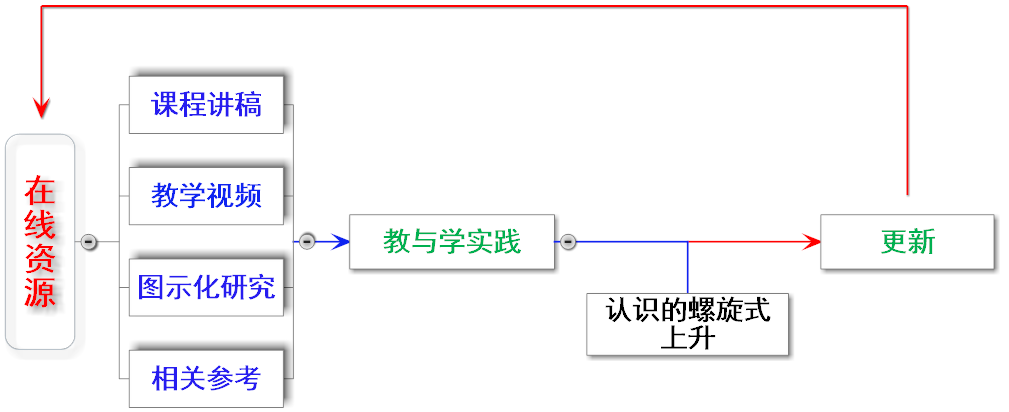
本课程的在线资源，主要包括：

（1）在线课程“微分流形上的微积分”，位于

复旦大学在线教育中心：http://fudan.mooc.chaoxing.com/portal

本课程在线课程网址：  

https://mooc1-.chaoxing.com/course/204042123.html

含有本课程的说明；网站按内容设定目录，含有内容的图示化研究、教学视频、讲稿、研讨内容、习题等。

（2）BiliBili网站，账号：manifoldflow-1

含有本课程的教学资源、图示化研究等

学习方法

 大学的学习应该注重理解与掌握知识体系的内在思想与方法，注重将知识升华为能力。对于知识体系自身的研究，我们概括为知识的通识化、方法化、思想化, 概述如下。

  知识的方法化  我们不应该学习就是为了考试、考试就是为了考试、考完基本全忘记, 而是应该将知识转化为认识世界的能力。就此我们建议将知识转化为方法。 所谓方法, 指可以系统性解决一类问题的思路与做法，方法对于问题的处理具有较为清晰的程序化流程. 获得方法的基础在于对同类问题的本质的认识, 我们将“本质” 称为“结构”。由于“相同的结构可以驱动不同的结论”，所以提炼可处理一类问题的方法也在于认识由结构驱动结论的具体方式。基于方法可以将知识转化为能力，表现为对所需研究的事物首先抽象为微积分等知识体系的研究对象， 然后利用对应的方法研究对应的性质，以期获得对所研究的事物的认识。

  知识的思想化  基于知识的方法化，可以进一步提炼方法的“驱动力”——思想. 简化、降维、变换、因果分解、抓住主要矛盾忽略次要矛盾等我们耳熟能详的认知世界的思想都在微积分中有着清晰而鲜明的表现。值得指出，在认识过程中相关思想驱动方法的提炼与发展，而对方法的深入研究又可能催生新的思想, 由此在学习过程中应该是方法化与思想化互为促进的进程。我们可以从知识的通识化、方法化、思想化这三个方面理解与掌握微积分知识体系。

 知识的通识化  我们将一门课程涉及的系统性思想与方法，称为知识体系。 对于一门知识体系，可以通过知识点分解知识体系，知识点为具有一定独立性的知识(思想与方法) 的集合。每一知识点再由若干知识要素组成，知识要素可为特定的数学等式、不等式或者特定的处理思想与方法, 亦称为“数学结构”。值得指出，隶属同一知识体系甚至不同知识体系的知识点可能包含相同的知识要素，称为数学通识。此外，知识体系之间亦可能存在“相似结构”，如一元微分学、高维微分学、赋范线性空间上微分学具有高度相似的知识点构成，均包括: 点列极限、映照极限、映照可微性、无限小增量公式、有限增量公式、逆映照定理与隐映照定理，主要结论的分析思想与方法也具有高度的统一性。既然，数学通识/相似结构为隶属同一知识体系或不同知识体系的知识点可能包含相同的知识要素，我们就可以基于数学通识/相似结构实现“同一知识体系之内的融会贯通”、“不同知识体系之间的触类旁通” 提供一种高成效的途径。值得指出，数学通识亦可服务于不同课程之间的衔接。在我们的教学中注重突出“数学通识”，表现为由“结构” 驱动“结论” 的知识体系发展方式，以此追求“温故而知新” 的教与学的成效。

对于本课程的学习，可以从微分流形上微积分知识体系的方法化、思想化、通识化这三个方面吸收知识、积累认识，最终获得这三个方面的系统性的提炼。

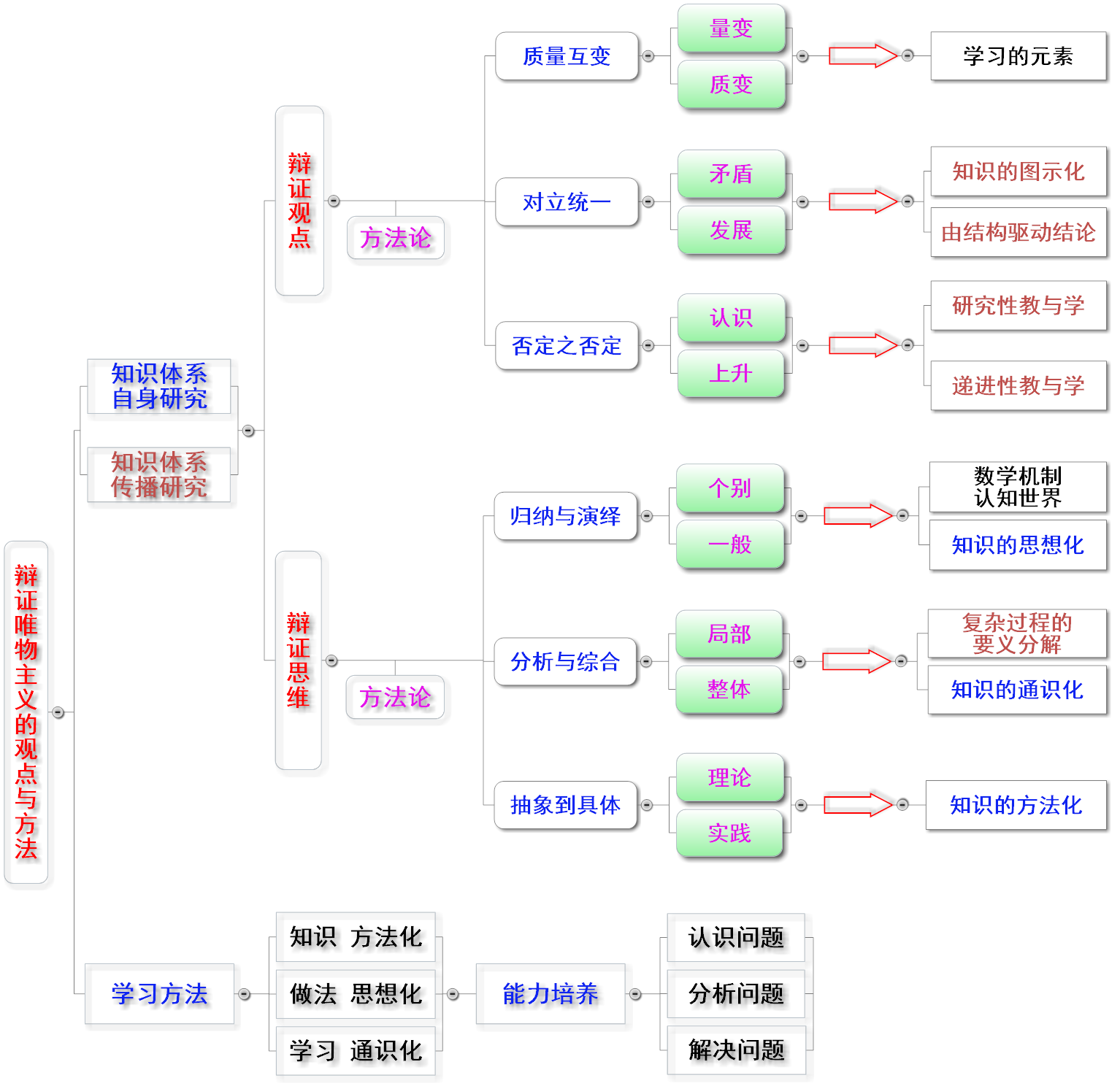
对于理工科课程，可以将辩证唯物主义的基本观点与方法融入整个教与学的过程—— 引领与具体指导建设一流课程：程度的一流化、成效的理想化，并且立德树人（三观引导）。作为基本观点的质量互变规律（不懂到懂、不会到会的学习元素）、对立统一规律（抓住事物的本质）、否定之否定规律（认识的螺旋式上升）；作为辩证思维的归纳与演绎（知识的思想化）、分析与综合（复杂过程的要义分解、知识的通识化）、抽象与具体（知识的方法化）在整个教与学中有着鲜明与具体的指导与实践，这不仅提升了教与学的质量，而且学生通过课程也体会并实践了辩证唯物主义的作为，将其作为世界观的主导。