控制系统数学建模及模型简化

数学模型是定量描述动力学系统的动态特性的数学表达式，它揭示了系统结构、参数与动态性能之间关系。

连续反馈系统常用数学模型包括微分方程、传递函数、状态方程等多种。常见的液压伺服系统多可分解为单输入—单输出（single-input-single-output， SISO）系统。

针对SISO系统，传递函数是工程实用性较强的数学模型。

传递函数不反映系统的物理结构。只要是系统动力学特性相似，不同的系统可以有相同或相似的传递函数。

实际上，在机电控制系统中，能够用电气校正环节进行系统特性校正的原因是动力学特性相似的系统可以有相同或相似的传递函数。

无论是动力学系统分析研究，还是控制系统分析与综合，动力学系统建模都是首要的前提条件。

建模方法

动力学系统的建模方法主要有两类，

一类是利用物理学原理建立系统参数间的关系，通过理论推导方式建立数学模型。

另一类是利用实验数据，通过分析系统输入与输出之间的数据关系，从而得到它的数学模型。

反馈控制系统也是一动力学系统。动力学系统建模方法同样适用于控制系统及控制系统各个组成环节的建模。可以用于描述动力学系统的各种方式同样适用于描述反馈控制系统及其各组成环节。

反馈控制系统是一种复杂的动力学系统。系统中组成要素较多，组成要素之间存在着复杂的相互作用或关联。其中有些相互作用是强作用，有些则属于弱作用。强作用对系统的特性影响较大，弱作用则不对系统整体特性产生较大影响。

突出系统要素间的强作用，忽略弱作用。依据系统组成要素间相互作用的特点可以将复杂大系统分解为相对简单的组成单元，即功能相对独立的单元。针对各个单元进行建模工作。然后将各个组成要素模型组装成复杂系统模型。这是一种实用化的系统分析与系统建模方法。

模型线性化

严格地说实际物理系统（特别是液压动力学系统）都包含不同程度的非线性因素，它们都是非线性系统。

在非线性因素较弱的情况下，可以忽略非线性因素，直接用线性模型替代非线性模型。这种有条件地将非线性数学模型化为线性数学模型的方法，称为非线性数学模型的线性化。

针对控制系统或其环节的线性化通常都是在它们的额定工作状态及与之对应的工作点的附近小范围内进行的。

依据级数理论，非线性方程可以在工作点处展开为泰勒级数。在偏差较小时，可以忽略二次项及高于二次的级数项。从而得到包含偏差一次项的线性函数式。

非线性模型线性化时，需要注意：

（1）实际工作物理系统为非线性系统。

（2）非线性系统在本质非线性处（不连续的非线性特性点）不能用上述线性化方法进行模型线性化。

（3）采用线性化得到的微分方程是增量微分方程。如。有时简化书写，去掉增量表示符号，简记为。注意简记后的方程仍然是增量方程。

模型化简

通常，控制系统分析与设计过程中的化简问题包括如下内容：

1）非线性系统模型线性化非线性模型的线性化是模型化简，将难处理的非线性控制问题化简为线性控制系统分析与设计问题。

2）方块图化简对描述控制系统的方块图进行化简，使其更为清晰反映控制系统主体结构或系统特性，便于开展系统分析与设计。严格说，对系统方块图的化简不算系统模型化简，因为系统模型并没有真实简化，只是系统方块图看起来明晰和简单了。

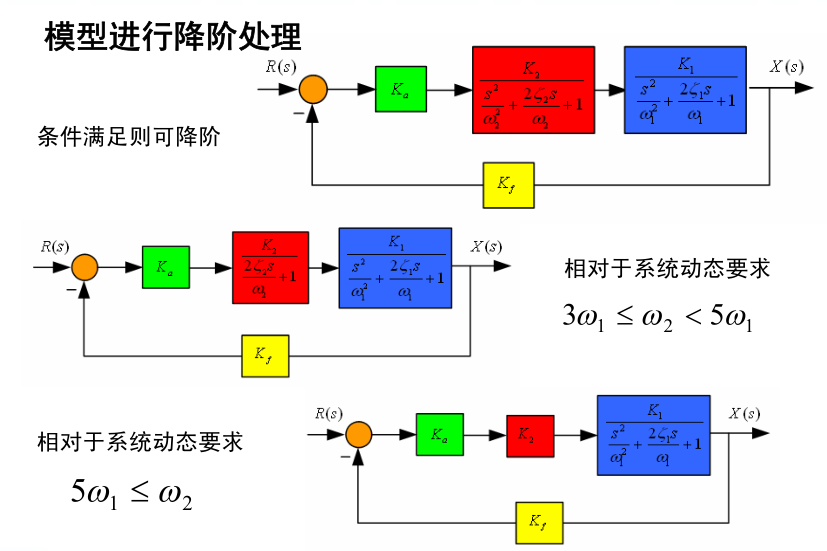
3）模型进行降阶处理