-
1 导读
-
2 教学PPT
-
3 教学视频
-
4 知识小测
轴向拉压变形强度计算
（1）拉压杆的内力计算 轴力图
1）内力的计算 如图3-8a所示的拉杆受两个力F作用，现用截面法求其内力：
图3-8 拉杆内力
∑Fx=0 FN－F=0 用截面m-m假想将杆截为两段，取左段为研究对象，并单独画出。同时，用内力FN表示右段对左段的作用，如图3-8b。根据平衡条件列出平衡方程如下
求得 FN = F
如果取右段为研究对象，如图3-8c所示，所得结果相同，即
FN′= F
FN和FN′是作用力与反作用力关系，即对同一截面来说，选取不同部分为研究对象，所得内力必等值、反向。
由于外力F 沿杆轴线方向，内力的合力FN也作用于轴线，称为轴力，如图3-8d所示。
轴力的正负号规定如下：轴力的正负号由杆件的变形确定，当轴力沿轴线离开截面，即与横截面外法线方向一致时为正，这时杆件受拉；反之轴力为负，杆件受压。一般未知指向的轴力可假设为正向，由计算结果判断其正负。
2）轴力图 工程上受拉、压的杆件往往同时受多个外力作用，称为多力杆。这时，杆上不同轴段的轴力将不同，为了清楚地表达轴力随截面的位置变化的情况，可以用轴力图来表示。轴力图的画法如下：
用平行于杆件轴线的坐标表示杆件截面位置，用垂直于杆件轴线的另一坐标表示轴力数值的大小，正轴力画在坐标轴正向，反之画在负向。
下面以例子来说明杆件内力的分析计算及轴力图的画法。
例3-1 汽车上某液压缸活塞杆受力如图3-9所示，设F＞F1＞F2，试求截面1-1、2-2的轴力并画轴力图。
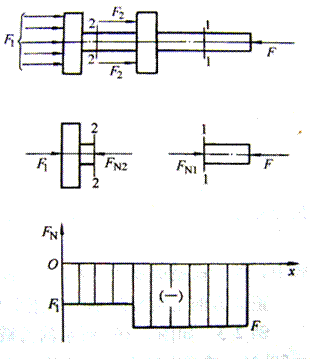
图3-9 活塞杆轴力图
解 ① 在活塞杆上以假想截面1-1将杆一分为二，取截面以右的一段为研究对象，并画其受力图，截面上轴力为FN1，如图3-9所示，根据平衡条件得
ΣFx=0 FN1－F=0
FN1 = F
② 在杆上取截面2-2 ，以截面以左的一段为研究对象，画其受力图如图3-10所示，根据静力平衡条件得
ΣFx=0 FN2－F1=0
FN2 = F1
③ 画轴力图：
以x轴表示杆上截面的位置，以纵轴表示轴力大小，FN1、FN2均为压力，画在坐标轴负向，如图3-9所示。
例3-2 汽车上某拉杆经简化后，受力及其大小分别如图3-10a所示，试作此杆轴力图。
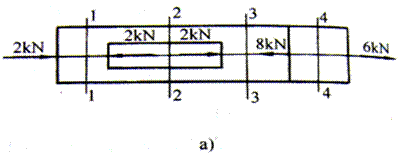
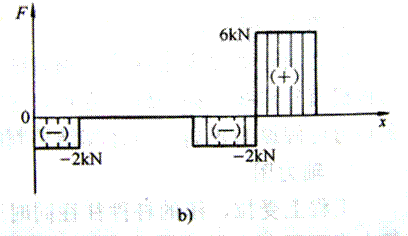
图3-10 汽车拉杆及受力图
解 ① 杆上作用有五个力，应将其分为四段来考虑，分别求出1-1、2-2、3-3和4-4截面的轴力如下
1-1截面 FN1 =2kＮ（压力）
2-2截面 FN2 =2－2=0
3-3截面 FN3 =8－6=2 kＮ（压力）
4-4截面 FN4 =6 kＮ（拉力）
② 根据求出的各截面的轴力画轴力图，如图3-10b所示。
(2) 拉、压杆横截面上的应力
根据前面的分析可知，利用截面法可以计算出杆件截面的内力大小，但是还不足以解决拉、压杆的强度问题。因为相同大小的内力作用于相同材料不同面积的截面上，效果是不一样的，杆件越细即截面面积越小，内力分布集度越大，越易拉断。因此，衡量杆件拉、压强度的，不是内力大小，而是应力大小。为了求出杆件横截面上任意一点的应力，必须了解内力在截面上的分布规律。任意一点的应力可以通过以下的拉伸试验观察、研究和推断：
取一等截面直杆，在杆件表面上作两条垂直于杆件轴线的直线ab和cd，如图3-11所示，然后在杆两端施加力F使其产生拉伸变形后发现，ab，cd分别平移到了a′b′ 和 c′d′，但仍保持为直线，且仍垂直于轴线。
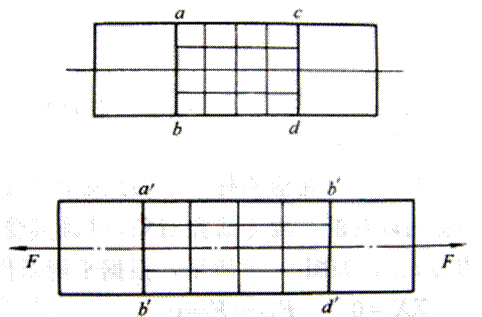
图3-11 拉伸试验
根据以上观察到的现象以及由表及里的分析，可作如下假设：变形前是平面的横截面，变形后仍为平面，变形时横截面只是沿轴线产生了相对平移。这一假设称为平面截面假设。设想杆件由许多纵向纤维组成，那么这一假设意味着杆件所有纵向纤维的伸长相等，由材料的均匀性假设可推断，各纵向纤维的受力也相等，也就是说，杆件横截面上的内力的分布是均匀的。由此得出结论：拉压杆横截面上各处应力大小相等，方向与内力FN方向一致，也就是说拉压杆横截面上只有正应力R，而无切应力τb。由于正应力R在横截面上的分布是均匀的，因此其计算公式为
R =FN /S0 （3-1）
式中，S0为横截面面积；FN为杆件横截面上内力；R为横截面上正应力。
正应力的正负号随轴力的正负号而定，即拉应力为正，压应力为负。
例3-3 如图3-12a所示的圆截面杆件AC，已知d1=20mm，d2=30mm，F1=20kN， F2=50kN，试画出轴力图并计算AB、BC段杆件截面上应力。
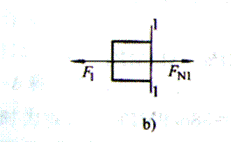
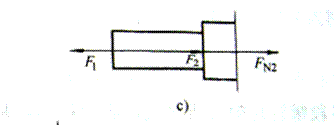
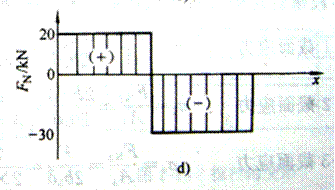
图3-12 杆件内力计算截面法及内力图
解 ① 在杆件AB段任取截面1-1，并取截面以左的一段为研究对象，画出受力图，如图3-12b所示，根据平衡条件求内力FN1
ΣFx=0 FN1－F1=0
FN1=F1=20kＮ
② 在杆件上BC段取截面2-2，并取截面以左一段为研究对象，画出受力图如图3-12c所示，根据平衡条件求内力ＦN2
ΣFx=0 FN2＋F2－F1=0
FN2=F1－F2=（20－50）kN = －30kN
③画轴力图如图3-12d所示。
④计算各段应力
AB段应力 R1=
=
=
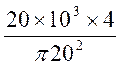=63.7MPa
BC段应力 R2=
=
=
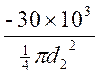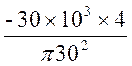= －42.4MPa
（3）许用应力
根据前面的分析，可由R＝
求出构件横截面上的应力，称为工作应力。但这仍不足以判断构件是否安全可靠，因为构件的强度与其材料的性能有关。
从拉伸试验结果可知，当材料的应力达到屈服强度ReL时，材料出现显著塑性变形；当应力达到强度极限Rm时，会引起断裂。显然，这两种情况都是不允许出现的。也就是说，构件工作时，其工作应力R必须小于ReL或Rm，这两个应力统称为极限应力，用R0表示。对于塑性材料，一般ReL＜Rm，因此R0=ReL，而对于脆性材料，则无ReL，因此R0=Rm。
在理想情况下，为了保证构件能安全可靠工作而又能充分利用材料的强度潜能，最好使设计的构件工作应力R小于且接近极限应力R0，但实际上很难做到这点。因为在设计构件时，作用在构件上的载荷难以估计，应力计算不完全正确，有一定近似性，同时材料不象假设的那样完全均匀，另外还要考虑构件磨损和各个构件的重要程度差异等因素。所以，必须使构件留有一定的安全储备，对材料的极限应力打个折扣，使构件工作应力的最大允许值等于材料极限应力的若干分之一，这个允许值称为许用应力，用符号［R］表示，即
［R］＝
式中，ｎ为大于1的系数，称为安全系数，用以表示构件安全储备的程度或强度的富余程度，因此得到不同材料的许用应力为
塑性材料［R］＝
脆性材料［R］＝
式中，安全系数ｎＳ、ｎb在常温和一般条件下取值范围分别为ｎs =1.4～1.8，ｎb=2.0～3.5。特殊情况下nＳ、nb可查阅有关资料手册。
正确选用合适的安全系数，可以设计出安全经济、尺寸合理的构件。
（4）强度条件及其应用
为了保证拉、压杆能安全工作，必须使杆件横截面上工作应力不超过材料在拉、压时的许用应力，即
R=
≤[R] (3-4)
式中ＦN为杆件危险截面（产生最大工作应力的截面）上的轴力；S0为危险截面初始面积。
式(3-4)称为拉、压杆的强度条件。在进行强度计算之前，须通过内力计算和画出轴力图，正确找出危险截面。如果危险截面强度足够，则其它截面也能安全工作。应用拉、压杆的强度条件可以解决工程中的以下三类问题：
1) 强度校核 当已知杆件横截面尺寸、杆件材料的许用应力[σ]以及杆件所受载荷时，可根据算出的工作应力R的大小与许用应力[R]比较，若满足R≤[R]则杆件强度足够。
2) 截面设计 若已知杆件所受载荷和材料的许用应力，可由式S≥
确定所需横截面面积，然后根据其他工程要求确定截面形状，进而确定截面的几何尺寸。
3) 确定承载能力 当已知杆件横截面尺寸和材料许用应力，可根据FN≤S[R]确定杆件所能承受的最大轴力，进而计算杆件所受外力的大小。
例3-4汽车离合器踏板如图3-21所示，已知踏板受到压力F1=400N，拉杆AB直径d=9mm，杠杆臂长L=330mm，=56mm，拉杆材料的许用应力[σ]=50MPa，试校核拉杆的强度。
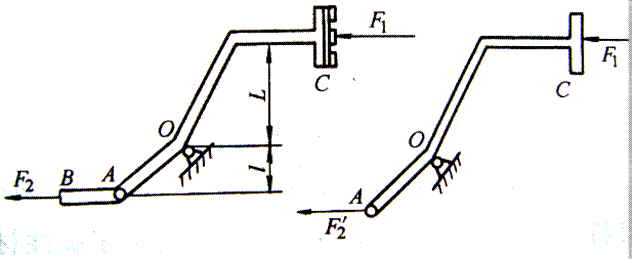
图3-21 汽车离合器踏板
解 ① 以杠杆AC为研究对象，画出受力图如图图3-21所示，根据平衡条件求拉力F 2′
∑Mo（F）=0 F1L－F2′
=0
F2′=
=
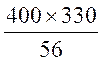N =2357 N
②校核拉杆强度。根据作用力与反作用力定律可知，拉杆所受拉力为F2= F2′，而且其轴力FN =F2=2357N，则其截面上正应力为
R==
=
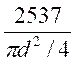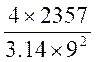MPa =37 MPa
由于工作应力R=37ＭPa<[R]=50ＭPa，所以拉杆的强度是足够的。
例3-5 汽车发动机活塞连杆组简图如图3-22所示，活塞上所受压力F=3.78×10 3kN，假设连杆BC横截面为矩形，高宽比为h：b=1.4，b≥173mm,材料许用应力[R]=90 MPa，连杆上所受压力F´近似等于FN，试设计连杆BC的截面尺寸h和b。
图3-22 求连杆截面尺寸
解 连杆上最大轴力等于活塞所受压力F，即有
FN=F=3.78×10 3kN
由强度条件得
S≥
= 
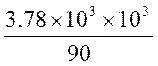mm2 = 42×103mm2
因为S =hb，且
=1.4，所以
1.4b2≥42×103 mm2
取b=173ｍｍ，则
h=1.4b=173×1.4ｍｍ=242ｍｍ
