连杆拉压变形分析

一、发动机连杆拉伸与压缩变形分析

在发动机故障分析中，常发现因发动机连杆变形而失效。在外力作用下，如何保证构件正常地工作而不致在使用寿命期限内失效，是构件承载能力分析所要研究的内容。如何分析构件的变形特点，并作出正确的强度计算，分析构件承载能力，是保证汽车及其他机器安全工作的重要问题。

足够的强度、刚度和稳定性是确保连杆具有足够承载能力的三个基本要求。构件在外力作用下的变形、失效破坏的规律、内力、应力和强度、刚度、稳定性计算等是承载能力分析计算的基本理论和方法。

1. 构件承载能力分析基础知识

（1）强度、 刚度、稳定性

构件抵抗破坏的能力称为强度。构件强度不够，会在工作中出现过大的塑性变形或断裂等现象，导致失效。

    构件抵抗变形的能力称为刚度。刚度不足的构件在工作中会出现过大的弹性变形，从而影响机械设备的正常运行。

    构件保持原有平衡状态的能力称为稳定性。一些受压的细长杆，如果稳定性不够，在工作中将不能始终保持原有的直线平衡状态而失控，例如活塞连杆组中的连杆。

足够的强度、刚度和稳定性是对构件提出的三个基本要求。使用好的材料和增大构件截面尺寸，可以满足构件承载能力的要求；但太好的材料和过大的构件截面尺寸势必造成构件成本的提高和重量的增加，使经济性下降。因此，构件安全性和经济性是一对矛盾，如何协调好这对矛盾，使设计出来的构件既安全实用又经济合理，正是构件承载能力分析要解决的关键问题。

  （2）变形固体及其基本假设

任何研究对象均有多方面的性质。就某一问题而言，这些性质中又有主、次之分，一些次要因素对所研究的问题影响甚微，则可不必考虑。因此，对不同学科需建立不同的理想化模型，对研究对象的属性进行概括。在静力分析中，为使问题简化，将研究对象抽象简化为“刚体”，忽略其变形因素。但在研究构件承载能力时，需要考察物体的受力、变形、失效的现象和规律，变形是主要因素。因此，应将研究对象看作变形固体。

实际变形固体的结构、形态很复杂，当考察宏观变形时，同样也应忽略其次要因素，对其作适当抽象，即作出以下基本假设：

    1）连续性假设  组成物体的物质毫无间隙地充满物体的几何容积。

    2）均匀性假设  物体各处的力学性能是完全相同的。

3）各向同性假设  物体沿各个方向的力学性能是相同的。

4）小变形假设  假设构件的变形量与其原来尺寸相比是很小的。

    根据这些假设，从宏观和统计学的角度来看，更能反映物体的主要性质。有了这些假设，在解决问题时，例如求物体的变形、位移等物理量时，可以用连续函数、微积分等数学工具解题。实践证明，经过这样的假设得出的理论和计算结果是足够精确的。但应指出，上述假设并不适用于所有材料。如某些高强度、超高强度钢材，对缺陷有强敏感性，不能适用连续性假设等。

    （3）杆件变形的基本形式

工程中构件的几何形状多种多样，但归纳起来大致可分为杆件、板件和箱体类零件。其中，杆件是指某一方向的尺寸远大于其余两方向尺寸的构件。在研究问题时，往往忽略构件外形因素，对其抽象、简化为计算简图，使问题简化。大量的工程构件可简化为杆件，如汽车传动轴、发动机中的连杆等。对轴线是直线，且各横截面都相等的杆件，称为等截面直杆（简称等直杆），它是构件承载能力的主要研究对象。

     当杆件受力形式不同时，发生的变形也各异，其基本形式可归纳为以下四种，即：轴向拉伸或压缩、剪切、扭转、弯曲等。这几种基本变形相应的受力及变形特征如图3-2所示。其它复杂的变形可归结为基本变形的组合，常见的组合变形有：拉（压）弯组合、弯扭组合、拉（压）扭组合变形，将在讨论基本变形的基础上进一步研究。

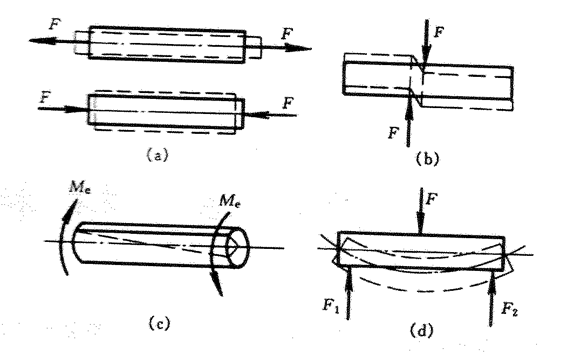
图3-2   基本变形

                                                                           a）轴向拉伸或压缩   b）剪切   c）扭转    d）弯曲

（4）内力   截面法和应力

     1）内力 构件工作中受到其它物体对它的作用力称为外力，包括主动力和约束反力。在外力的作用下，会引起物体内部各质点之间的相对位置以及相互作用力发生改变，表现出来就是构件发生了变形，构件内部质点之间相互作用力（固有内力）的改变量称为附加内力，简称内力。内力随外力的大小而变化，当内力达到某一极限值时，构件即发生破坏。因此，构件的内力大小及其分布方式与其承载能力之间有密切的关系，研究和分析内力是解决强度、刚度等问题的基础。

2）截面法  截面法是分析、计算内力的方法，就是假想用一截面把构件截为两部分，取其中一部分为研究对象，并以内力代替另一部分对研究部分的作用，根据研究部分内力与外力的平衡确定内力大小和方向。

    如图3-3所示，杆件在外力F₁、F₂、F₃的作用下平衡，欲求杆件的内力。可用一假想的截面m-m将杆件一分为二，任取其中一段来研究。由于杆件处于平衡状态，因此其中任一段也应平衡，这时可利用静力平衡条件来列出平衡方程，求出截面m-m上的内力。

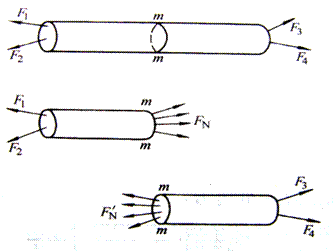
图3-3  截面法

    如图3-4a所示，在杆件截面上任一点K周围，取一微面积△S，△S上内力的合力为△F，则它们的比值为 3）应力  截面法可以确定杆件截面上内力的合力，但不能确定内力在截面上的分布密度，由此需引入应力的概念。

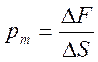
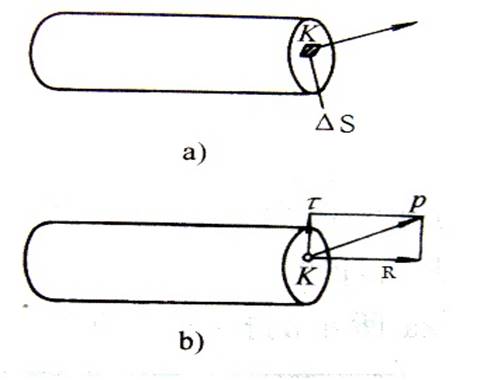
图3-4   应力概念

   式中，p_m称为△S平均应力。一般内力不是均匀分布的，这时，平均应力p_m随△S的大小而变化，它不能反映内力分布的真实情况。为确切地反映K点处的内力集度，将△S减小，当△S趋于零时，得

式中，p称为K点的全应力，它表明了内力系在K点的集度。p是一个矢量，通常把p分解为两个正交的分量：垂直于截面的分量R称为正应力，切于截面的分量τ_b称为切应力，如图3-5b所示。

    应力的单位是Pa（帕），1Pa=Ｎ/ｍ²。在工程实际中还常用MPa和GPa ，其换算关系为1M Pa = 10⁶Pa，1 GPa=10⁹Pa。

2. 杆件的轴向拉伸与压缩

当杆件所受外力的作用线与杆件轴线重合时，杆件将沿轴线伸长或缩短，称为轴向拉伸和压缩。这类杆件称为拉压杆。如图3-5汽车发动机中的连杆，按简化力学模型分析，所受外力的合力与轴线重合，杆件发生拉伸或压缩变形。工程实际中，气缸体与气缸盖的联接螺栓（图3-6）、螺旋千斤顶的螺杆（图3-7）等，都可以简化为轴向拉伸和压缩计算简图。

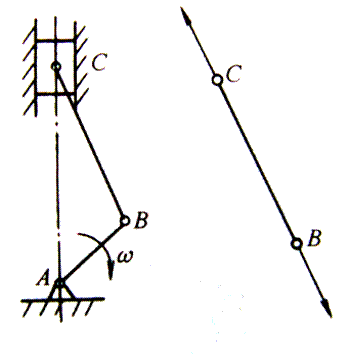
     图3-5   活塞连杆组

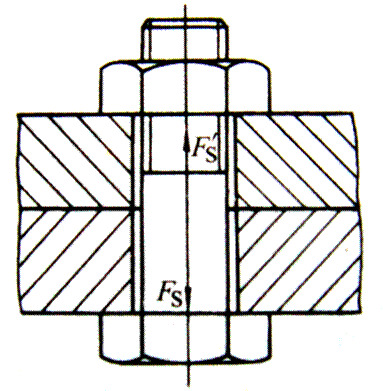
图3-6   螺栓

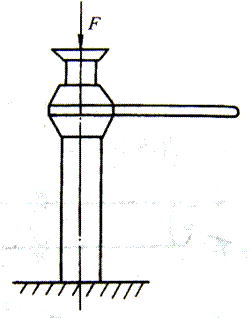
图3-7   螺旋千斤顶