【课程理念】

本节课主要在学科本质和学科价值两方面进行学科专业探索。高中新一轮课改强调发展学生的数学核心素养，而数学抽象位于六大核心素养之首，也说明抽象是数学的本质特征。哥尼斯堡七桥问题很好地体现了数学抽象的过程、方法和价值，所以借此例进行学科本质教学。另外，学生普遍对学习数学的意义认识模糊，这直接导致学生数学观的扭曲，也会影响未来职业发展，所以我从数学之用与数学之美两方面、结合丰富的素材多角度向学生展示数学的学科价值。

【学习目标】

1.了解数学学科体系和学科要求；

2.通过哥尼斯堡七桥问题体会数学抽象的过程和方法；

3.通过观看视频体会数学知识的应用广泛；

4.通过语言文学实例感受数学思想的迁移常见；

5.通过数学实例感受数学之美。

【学习过程】

一、学科体系

学科门类：07 理学

一级学科：0701 数学

二级学科：070101 基础数学

          070102 计算数学

          070103 概率论与数理统计

          070104 应用数学

          070105 运筹学与控制论

二、学科要求

数学所需智能：逻辑智能、空间智能、自省智能。

业务培养要求：受到严格的数学思维训练；掌握计算机的原理和运用手段；培养从事数学教学基本能力和数学教育研究、数学教学研究、数学科学研究、数学实际应用等基本能力．

专业主干课程：数学分析、高等代数、解析几何、微分几何、高等几何、常微分方程、偏微分方程、概率论与数理统计、复变函数论、实变函数论、抽象代数、近世代数、数论、泛函分析、拓扑学、模糊数学。师范类还要学习数学教育学等。

实践性教学环节：包括计算机的实际操作，深入一线教学实践。

三、学科本质

师：我们很早就接触数学，如果让大家用一个词概括数学的学科特点，应该是什么？

引导学生达成共识：抽象。

师：我们看到三个人、三匹马、三块石头、三棵树，当人们从这些具体的物质形态中抽象出“3”，才形成了数学，所以说，没有抽象，就没有数学。

师：为了更清楚的让大家体会数学抽象的过程和方法，我们来看“哥尼斯堡七桥问题”：

哥尼斯堡是欧洲一个美丽的小城，有一条河横贯其中，河中间有两座岛，连接岛和岸有七座桥，人们经常在此散步。有一天，有人提出这样的问题：能否不重复的走遍这七座桥？于是，人们进行了各种尝试，发现不是一座桥走了两遍，就是有的桥没有走过。有人说这样的路线不存在，也有人说这样的路线存在只是一时还没有找到，就在大家莫衷一是时，人们想到了可以写信求助大数学家欧拉。欧拉收到这封信，发现这个问题用已有的数学方法是不能解决的，于是研究采用了新的方法，一举解决了这个问题，并开启了“图论”这一数学分支。

师：现在我们和欧拉一起解决这个问题：

首先，

欧拉对图形做了抽象：抽象成点线图。

欧拉对问题做了抽象：抽象成“一笔画问题”。

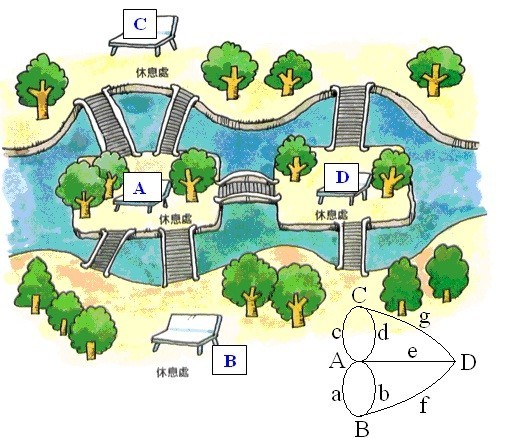
接下来，

问1：欧拉把图形上的点分成两类，如果是你，会分成哪两类？

生：按照连接点的边数是奇数还是偶数分成两类。

问2：为了“一笔画”成功，是偶结点多一些好，还是奇结点多一些好？

生：偶结点多一些好。

问3：奇结点少到几个才能“一笔画”？

生：奇结点为0或2个才能“一笔画”。

师：我们得到了“一笔画问题”的结论：如果一个图是连通的，并且奇结点的个数是0或2个，那么它可以一笔画出，否则不能。

师：我们用这个结论不仅可以解决哥尼斯堡七桥问题，还能解决与此相关的一类问题。

1.能否一笔画写出“串”字？

2.能否一笔画画奥运五环？

师：借助此例，我们能否总结数学抽象的过程与方法？

师引导学生得出共识：

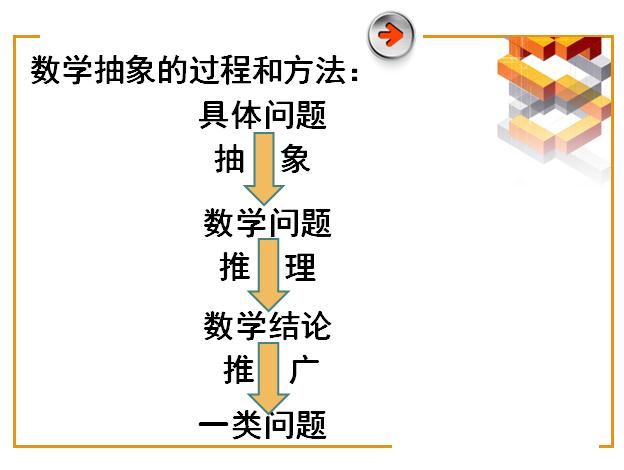
四、学科价值

师：我们为什么要学习数学？

1、数学知识的应用广泛

素材一：《唐老鸭漫游数学奇境》

        数学可以用于音乐、艺术作品、建筑、机械、天文等多个学科。

素材二：游思彬的演讲《数学有用》

        数学是扶大厦之将倾的力量，它能力挽狂澜。

        数学是国之兴亡的后盾。

        数学是通往星辰大海的密钥，是国防科技的护盾，是我们脚下这片土地的未来。

2、数学思想的迁移常见

素材三：李商隐的《瑶池》

瑶池阿母绮窗开，

黄竹歌声动地哀。

八骏日行三万里，

        穆王何事不重来？        

              这首诗是唐朝诗人李商隐借周穆王讽刺唐朝皇帝贪求长生不老，诗文大意

         是：“王母打开了华丽的窗帘，仙女们高唱着 ‘黄竹哀歌’等待着穆王的到来。

         周穆王乘坐的是由八匹神马拉的车子，一天可行三万里，往来瑶池应该十分方便。

         但是穆王终于没有重来，这是为什么呢？”这首诗的后两句体现了数学的反证法。

素材四：赵本山的小品《卖拐》

“脑袋大，脖子粗，不是大款就是伙夫！”

             通过某些人脑袋的大小和脖子的粗细和大款、伙夫一致从而得出结论，他们的

         其他方面也一样，这句话蕴含了类比的推理方法。

3、追寻数学之美是数学最高层次的价值

素材五：请大家欣赏从不同途径导出0.618

    途径1：黄金分割，它是公认的最具美感的分点，位于0.618的位置；

    途径2：由斐波那契数列{1,1,2,3,5,8,13,21,34,55,89，…}组成的分数数列通项的

           极限值是0.618；

    途径3：黄金矩形的宽长之比是0.618；

    途径4：华罗庚优选法的实验点是0.618。

    师总结：通过此例我们看到了世界的多样性与统一性，看到了数学的“统一美”。

素材六：圆周率钢琴曲

            圆周率是一个无限不循环小数，把圆周率中的数字逐一翻译成“音符”得到了

        美妙的钢琴曲。

素材七：分形艺术欣赏

             分形艺术是借助计算机将数学公式反复迭代运算，再结合作者的艺术性塑造所

         产生的作品，分形几何让人们感悟到科学与艺术的融合。

结束语：数学是一门无比美妙的学科，同学们，进一步探索数学世界，你们准备好了吗？