
关联规则挖掘发现大量数据中项集之问有趣的关联或相关联系。随着大量数据不停地收集和存储,许多业界人士对于从他们的数据库中挖掘关联规则越来越感兴趣。从大量商务事务记录中发现有趣的关联关系,可以帮助许多商务决策的制定,如分类设计、交义购物和贱卖分析。

关联规则挖掘的一个典型例了是购物篮分析。该过程通过发现顾客放入其购物篮中不同商品之间联系,分析顾客的购买习惯。通过了解哪些商品频繁地被顾客同时购买,这种关联的发现可以帮助零售商制定营销策略。例如,在同一次去超级市场,如果顾客购买牛奶,他也购买面包(和什么类型的面包)的可能性有多大?通过帮助零售商有选择地经销和安排货架,这种信息可以引导销售。例如,将牛奶和面包尽可能放近一些,可以进一步刺激一次去商店同时购买这些商品。
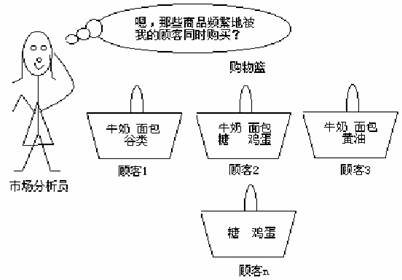
(1)相关概念:
设 I={I1, I2,…,Im}是项的集合。
◇ 事务数据:任务相关的数据D是数据库事务的集合,其中每个事务T是项的集合,每一个事务有一个标识符,称作TID。
◇ 项集:项的集合称为项集。每一个TID都是项集。
◇ k-项集:包含k个项的项集称为k-项集,如:{面包,牛奶}就是一个2-项集。
◇ 关联规则:关联规则是形如A→B的蕴涵式,其中A∈I, B∈I,并且A∩B=Φ。
◇ 支持度s:规则A→B在事务集D中成立,具有支持度s,其中s是D中事务包含A∪B(即,A和B二者)的百分比。它是概率s(A→B)=P(A∪B)。
◇ 置信度c:规则A→B在事务集D中成立,如果D中包含A的事务同时也包含B的百分比就是置信度c。confidence(A→B)=P(B|A)。
◇ 项集出现频率:是包含项集的事务数,简称项集的频率、支持度计数或计数。
◇ 频繁项集:如果项集满足最小支持度,则称它为频繁项集。频繁k-项集的集合通常记作Lk。
◇ 强规则:同时满足最小支持度阈值(min_ sup)和最小置信度阈值(min_conf)的规则称作强规则。
(2)关联规则挖掘步骤
“如何由大型数据库挖掘关联规则?”关联规则的挖掘是一个两步的过程:
◇ 找出所有频繁项集:根据定义,这些项集出现的频繁性至少和预定义的最小支持计数一样。
◇ 由频繁项集产生强关联规则:根据定义,这些规则必须满足最小支持度和最小置信度。如果愿意,也可以使用附加的兴趣度度量。这两步中,第二步最容易。挖掘关联规则的总体性能由第一步决定。
(3)Apriori算法
Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法。算法的名字基于这样的事实:算法使用频繁项集性质的先验知识。Apriori使用一种称作逐层搜索的迭代方法,k-项集用于探索(k+1)-项集。首先,找出频繁1-项集的集合。该集合记作L1。L1用于找频繁2-项集的集合L2,而L2用于找L3,如此下去,直到不能找到频繁k-项集。找每个Lk需要一次数据库扫描。

(4)Apriori算法性质
◇ 连接:通过将Lk-1(所有的频繁k-1项集的集合)与自身连接产生候选k项集的集合。
◇ 剪枝:如果某个候选的非空子集不是频繁的,那么该候选肯定不是频繁的,从而可以将其从CK中删除。

示例:购物篮分析
让我们看一个Apriori的具体示例。该例基于AllElectronics的事务数据库。数据库中有9个事务,即D= 9。Apriori假定事务中的项按字典次序存放,如下图所示。

解析:我们使用下图来解释Apriori算法发现D中的频繁项集的过程。
(1)找出所有频繁项集
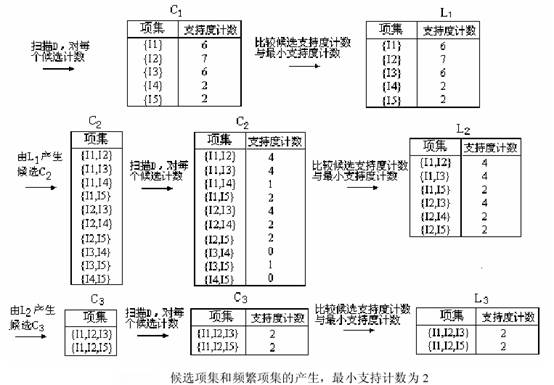
注意:由L2产生C3时,并没有{ I1,I2,I4},这是因为{ I1,I2,I4 }如果是频繁的,那么{I1,I2,I4 }的非空子集一定是频繁的,显然{ I1,I4 }不是频繁的,所以被剪枝掉了。

(2)由频繁项集产生强关联规则
满足最小支持度2的频繁项集有:L1={I1,I2,I3}和L2={I1,I2,I5},置信度公式为: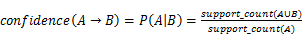 。
。
L2={I1,I2,I5}的非空子集为:{I1,I2},{I1,I5},{I2,I5},{I1},{I2},{I5},关联规则如下,列出置信度。
I1∧I2→I5 confidence= 2/4 = 50%
I1∧I5→I2 confidence = 2/2 =100%
I2∧I5→I1 confidence = 2/2 =100%
I1→I2∧I5 confidence = 2/6 = 33%
I2→I1∧I5 confidence = 2/7 = 29%
I5→I1∧I2 confidence = 2/2 =100%
如果最小置信度阈值为70%,则L2只有2, 3和最后一个规则可以输出,因为只有这些是强的。而L1={I1,I2,I3}的非空子集为:{I1,I2},{I1,I3},{I2,I3},{I1},{I2},{I3}
I1∧I2→I3 confidence= 2/4 = 50%
I1∧I3→I2 confidence= 2/4 = 50%
I2∧I3→I1 confidence= 2/4 = 50%
I1→I2∧I3 confidence = 2/6 = 33%
I2→I1∧I3 confidence = 2/7 = 29%
I3→I1∧I2 confidence = 2/6 = 33%
如果最小置信度阈值为70%,则L1没有规则可以输出。



















