
1、物以类聚,人以群分,从五眼联盟出发,浅谈意识形态与中国的朋友圈。
2、根据全国各省份数据进行聚类分析,感受国家西部大开发战略。


将物理或抽象对象的集合分组成为由类似的对象组成的多个类的过程被称为聚类。由聚类所生成的簇是一组数据对象的集合,这些对象与同一个簇中的对象彼此相似,与其他簇中的对象相异。在许多应用中,一个簇中的数据对象可以被作为一个整体来对待。
聚类分析是一种重要的人类行为。早在孩提时代,一个人就通过不断地改进下意识中的聚类模式来学会如何区分猫和狗,或者动物和植物。聚类分析已经广泛地用在许多应用中,包括模式识别,数据分析,图像处理,以及市场研究。通过聚类,一个人能识别密集的和稀疏的区域,因而发现全局的分布模式,以及数据属性之间的有趣的相互关系。
(1)距离与相似系数
距离是聚类分析常用的分类统计量。两个样品间的距离在【0,∞】之间,距离越小,两个样品越接近。在聚类分析中,最常用的距离如下:
◇ 绝对距离: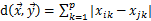
◇ 欧氏距离: 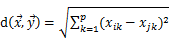
◇ 明氏距离: 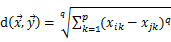
◇ 切氏距离: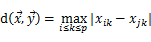
◇ 兰氏距离 ( Lance、Willims):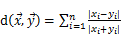
◇ 马氏距离: 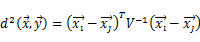 ,其中:
,其中: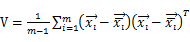 ,
,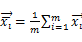
(2)分层聚类法
分层聚类法,又称为系统聚类法,或谱系聚类法,是聚类分析诸方法中用得最多的一种。它分为聚集法和分割法。聚集法的基本思想是:开始将样品各自作为一类,将最“靠近”的首先进行聚类,再将这个类和其他类中的最“靠近”的结合,这样继续合并直至所有对象都综合成一类或满足一个阈值条件为止。分割法正好相反,先将对象看成一大类,然后割成两类,使一类中的对象尽可能地“远离”另一类的对象;再将每一类继续这样分割下去,直至每个对象都自成一类或满足一个阈值条件为止。
分层聚类的具体方法有很多,最短距离法、最长距离法、中间距离法、重心法、类平均法、变差平方和法等等。我们这里以最短距离法为例。
最短距离法又称单一连接或最近邻连接。两个类之间的距离如果定义为两类中元素之间距离最小者(见下图),并依此逐次选择最“靠近”的聚集的方法叫最短距离法。
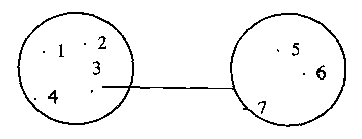
最短距离法中的类间距
类间距离d{1,2,3,4}{5,6,7}=min{d15,d16,d17,d25,d26,d27,d35,d36,d37,d45,d46,d47}=d37。

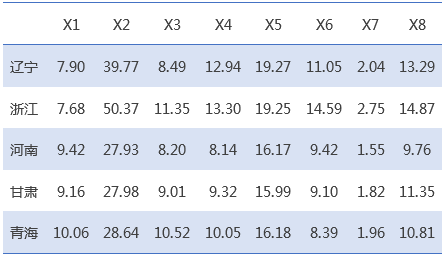
示例:下表是1991年5省份城镇居民月人均消费数据,其中,x1:粮食支出、x2:副食支出、x3:烟酒茶支出、x4:其他副食支出、x5:服装支出、x6:日用品支出、x7:燃料支出、x8:非商品支出。请你用最短距离法对下面的城市进行聚类。
解析:
(1)计算n个样品两两间的距离{dij},记作D={dij}。
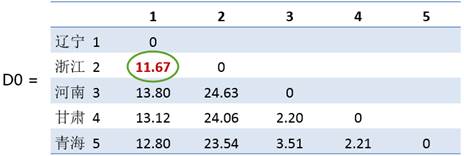
其中,采用欧氏距离计算距离矩阵中的每个值,即高中学过的两点间距离公式。如,
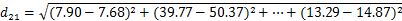
= 11.67
(2)构造n个类,每个类只包含一个样品。
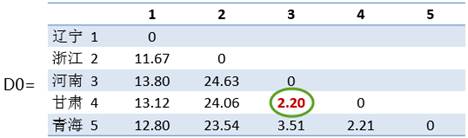
开始有五个类:G1={辽宁 1},G2={浙江2},G3={河南 3},G4={甘肃 4},G5={青海5}。
(3)合并距离最近的两类为一个新类。D0中最小值是G (4,3) = 2.20。即将类G3和G4合并成一新类G6={3,4}。
(4)计算新类与当前各类的距离。若类的个数为1,转到步骤 (5),否则回到步骤(3)。
计算新类G6与G1、G2、G5之间的距离。利用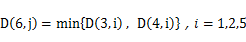 计算得:
计算得: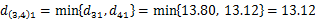
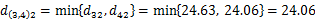
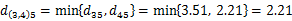
故,在距离矩阵D0中消去了3、4所对应的行和列,并加上{3,4}这一新类对应的一行一列,得到新距离矩阵D1。如下图所示。
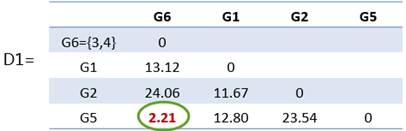
在D1中发现类间最小距离为d65=2.21,合并类G6和G5得到新类G7,G7={6,5}={3,4,5},再利用 ,计算得:
,计算得:
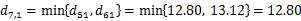
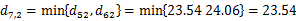
故得到新的距离矩阵:
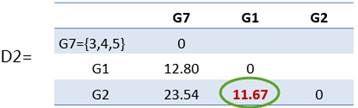
新矩阵类的个数不等于1,重复步骤 (3)
类间最小距离是d12=11.67,合并G1和G2得到新类G8={1,2}。此时,我们只有两个不同的类G7={3,4,5}和G8={1,2},它们的距离是:d78=min{d71, d72}={12.80,23.54}=12.80。最后,得到新的距离矩阵:

从而,类G7={1,2,3}和G8={1,2}合并为一个含全部5个样本{1,2,3,4, 5}的类,其最短距离是12.80。类的个数为1,算法结束。
(5)画出谱系聚类图
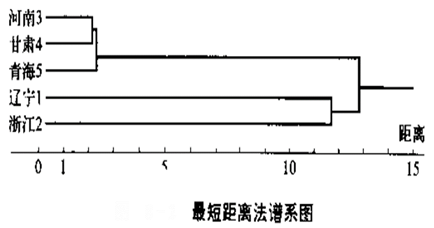
(6)决定类的个数和类别。
听取专家意见,确定阈值,并根据阈值确定聚类的个数和类别。


















