1.  能阐述朴素贝叶斯分类原理

2.  能阐述决策树分类原理，及C45算法思想

3.  能用Weka软件进行贝叶斯分类和C45决策树分类，并正确分析结果

4.  能使用Python编程实现决策树分类，并正确分析结果

1、新冠地区疫情风险等级分类案例分析，探讨中国制度的优势。

2、经济发展中，对于不同的客户数据分析，将客户的购买行为进行分类。

数据分类是一个两步过程，第一步，建立一个模型，描述预定的数据类集或概念集。通过分析由属性描述的数据库记录来构造模型。第二步，使用模型进行分类。

（1）朴素贝叶斯

朴素贝叶斯的思想是这样的：如果一个事物在一些属性条件发生的情况下，事物属于 A 的概率>属于 B 的概率，则判定事物属于 A。

通俗来说比如，你在街上看到一个黑人，我让你猜这哥们哪里来的，你十有八九猜非洲。为什么呢？在你的脑海中，有这么一个判断流程：

① 这个人的肤色是黑色 <特征>

②黑色人种是非洲人的概率最高 <条件概率：黑色条件下是非洲人的概率>

③ 没有其他辅助信息的情况下，最好的判断就是非洲人。

这就是朴素贝叶斯的思想基础。

再扩展一下，假如在街上看到一个黑人讲英语，那我们是怎么去判断他来自于哪里？提取特征：

① 肤色：黑

②语言： 英语

③ 黑色人种来自非洲的概率： 80%

 黑色人种来自于美国的概率：20%

④ 讲英语的人来自于非洲的概率：10%

 讲英语的人来自于美国的概率：90%

在我们的自然思维方式中，就会这样判断：

这个人来自非洲的概率：80% * 10%= 0.08

这个人来自美国的概率：20% * 90%=0.18

我们的判断结果就是：此人来自美国！

（2）贝叶斯定义与贝叶斯分类

贝叶斯的数学原理如下：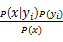

朴素贝叶斯正式定义如下：

①设x={a₁,a₂,…,a_m}为一个待分类项，而每个a为x的一个属性。

②有类别集合C={y₁,y₂,…,y_n}。如果n=2，就是分两类。

③ 计算P(y₁|x),P(y₂|x), … , P(y_n|x)。

④如果P(y_k|x) = max{P(y₁|x), P(y₂|x), … , P(y_n|x)}，则x∈y_k

那么，现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做：

①找到一个已知分类的待分类项集合，这个集合叫训练样本集

② 统计得到在各类别下各特征属性的条件概率估计。

③ 如果各特征属性是条件独立的，则贝叶斯定理公式为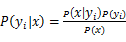：，因为分母对于所有类别为常数，因此将分子最大化皆可。

可以看到，整个朴素贝叶斯分类分为三个阶段：

第一阶段——准备工作阶段，这个阶段的任务是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。

第二阶段——分类器训练阶段，这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。

第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，由程序完成。

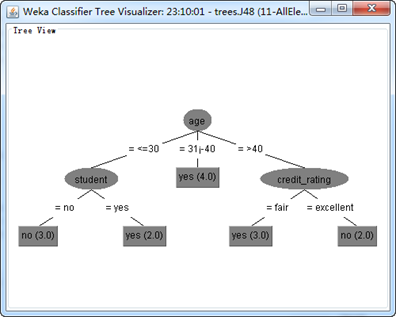
例题1：下表数据是取自AllElectrionics顾客数据库数据记录训练集，类标号属性购买电脑顾客数据记录训练集有两个不同的类（是，否），因此由此形成了训练样本的两个类，在训练集中有14个样本，两个类中分别有9个和5个样本。

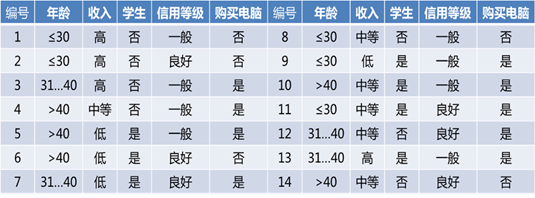
根据上表，判断未知样本X={30岁以下,中等收入，学生，信誉一般}，应属哪一类？是否会购买电脑？

解析：

根据贝叶斯公式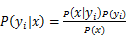：，y_i（i=1,2）有两个类，即y1=是，y2=否。两类的分母都一样，所以只需要判断分子即可。

P( 购买电脑 =“是” ) = 9/14 = 0.643        // 分子右侧的P(y1)

P( 购买电脑 =“否” ) = 5/14 = 0.357        // 分子右侧的P(y2)

P( 年龄≤30 | 购买电脑 =“是”) = 2/9 = 0.222

P( 年龄≤30 | 购买电脑 =“否”) = 3/5 = 0.600

P( 中等收入 | 购买电脑 =“是”) = 4/9 = 0.444

P( 中等收入 | 购买电脑 =“否”) = 2/5 = 0.400

P( 学生 =“是” | 购买电脑 =“是”) = 6/9 = 0.667

P( 学生 =“是” | 购买电脑 =“否”) = 1/5 = 0.200

P( 信用等级 =“一般”| 购买电脑 =“是”) = 6/9 = 0.667

P( 信用等级 =“一般”| 购买电脑 =“否”) = 2/5 = 0.400

P(X | 购买电脑 =“是”) = 0.222×0.444×0.667×0.667 = 0.444  // 分子左侧P(x | y1)

P(X | 购买电脑 =“否”) = 0.600×0.400×0.200×0.400 = 0.019 // 分子左侧P(x | y2)

P(X | 购买电脑 =“是”) P(购买电脑 =“是”) = 0.444×0.643 = 0.028  // 整个分子

P(X | 购买电脑 =“否”) P(购买电脑 =“否”) = 0.019×0.357 = 0.007  // 整个分子

结论：未知样本X={30岁以下,中等收入，学生，信誉一般}属于第1类，即买电脑。

决策树的基本原理是采用概率论原理，用决策点代表决策问题，用方案分枝代表可供选择的方案，用概率分枝代表方案可能出现的各种结果，经过对各种方案在各种结果条件下损益值的计算比较，为决策者提供决策依据。

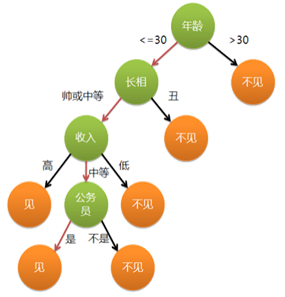
通俗来说，决策树分类的思想类似于找对象。下面的对话场景：

女儿：多大年纪了？        母亲：26。

女儿：长的帅不帅？        母亲：挺帅的。

女儿：收入高不？          母亲：不算很高，中等情况。

女儿：是公务员不？        母亲：是，在税务局上班呢。

女儿：那好，我去见见。

     这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别：见和不见。假设这个女孩对男人的要求是：30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员，那么这个可以用下图表示女孩的决策逻辑。

WEKA的全名是怀卡托智能分析环境（Waikato Environment for Knowledge Analysis），同时weka也是新西兰的一种鸟名，而WEKA的主要开发者来自新西兰。WEKA作为一个公开的数据挖掘工作平台，集合了大量能承担数据挖掘任务的机器学习算法，包括对数据进行预处理，分类，回归、聚类、关联规则以及在新的交互式界面上的可视化。

用WEKA软件实现例题1的可视化视图如下：