1、加权平均值，由成绩绩点出发——看问题，抓关键。
2、集中统计分析与“化繁为简”的人生策略。
用统计指标对定量数据进行统计分析，常从集中趋势和离散趋势两个方面进行分析。平均水平的指标是对个体集中趋势的度量。使用最广泛的是均值和中位数；反映变异程度的指标是对个体离开平均水平的度量，使用较广泛的是标准差（方差）、四分位间距。
（1）算术平均数
算术平均数，又称均值，是统计学中最基本、最常用的一种平均指标，分为简单算术平均数、加权算术平均数。它主要适用于数值型数据，不适用于品质数据。算术平均数是加权平均数的一种特殊形式（特殊在各项的权重相等）。在实际问题中，当各项权重不相等时，计算平均数时就要采用加权平均数；当各项权相等时，计算平均数就要采用算术平均数。
算术平均数的计算公式为：mean(x)=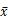
=
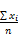，在EXCEL中可以用average函数。
例题1：有如下8个整数：23，29，20，32，23，21，33，25。求其算术平均值。
解析：avg=(23+29+20+32+23+21+33+25)/8= 25.75。
加权平均数的计算公式为：mean(x)=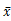
=
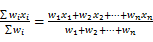
例题2：小升初，考数学、外语、语文。计分原则：数学权重为2，外语语文为1。张三得分分别为：数学95、外语80、语文85。求张三的平均分。
解析：avg=(95*2+80*1+85*1) / ( 2+1+1 )= 88.88。
（2）调和平均数
又称倒数平均数，是总体各统计变量倒数的算术平均数的倒数。调和平均数的计算公式为：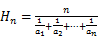
。在EXCEL中可以用HARMEAN函数。
例题3：市场买菜5种，黄瓜4元/千克，西红柿5元/千克，土豆2元/千克，茄子4元/千克，冬瓜3元/千克。现每样蔬菜均买10元钱的，求蔬菜每千克多少钱？
解析：
蔬菜总量：黄瓜10/4千克，西红柿 10/5千克，….，共计：10(1/4+1/5+1/2+1/4+1/3)千克
蔬菜总价格：每样素材各10元，共50元
均值：50/10 ( 1/4+1/5+1/2+1/4+1/3 )=3.26
加权调和平均数是加权算术平均数的变形。它与加权算术平均数在实质上是相同的，而仅有形式上的区别，即表现为变量对称的区别、权数对称的区别和计算位置对称的区别。因而其计算公式为：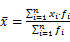
。
例题4：市场买菜5种，黄瓜4元/千克，买10块钱的，西红柿5元/千克，买15块钱的，土豆2元/千克，买5块钱的，茄子4元/千克，买12块钱的，冬瓜3元/千克，买9块钱的。求蔬菜每千克多少钱？
解析：
蔬菜总量：10/4+15/5+5/2+12/4+9/3=14千克
蔬菜总价格：10+15+5+12+9=51元
均值：51/14=3.64
（3）几何平均数
几何平均数是对各变量值的连乘积开项数次方根。求几何平均数的方法叫做几何平均法。如果总水平、总成果等于所有阶段、所有环节水平、成果的连乘积总和时，求各阶段、各环节的一般水平、一般成果，要使用几何平均法计算几何平均数，而不能使用算术平均法计算算术平均数。几何平均数也分为简单几何平均数和加权几何平均数两种形式。
计算几何平均数要求各观察值之间存在连乘积关系，它的主要用途是：
◇对比率、指数等进行平均；
◇计算平均发展速度；其中：样本数据非负，主要用于对数正态分布。
◇复利下的平均年利率；
◇连续作业的车间求产品的平均合格率。
几何平均数的公式为
，在EXCEL中，可以用GEOMEAN函数。
例题5：某国1996-2000年的增长速度分别为：117%、110%、109%、108%、107.8%，求5年间平均发展速度。
解析：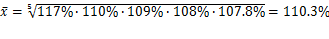
（4）位置平均数
◇众数：是样本观测值在频数分布表中频数最多的那一组的组中值。通俗地讲，出现次数最多的数就是众数，当然众数也可能有多个，甚至没有（所有数据出现的次数都一样）。在EXCEL中，可以用MODE.SNGL函数。
例题6：有如下8个数，23，29，20，32，23，21，33，25。求众数。
解析：众数=23，出现2次。
◇中程数：又称中列数，是一组统计数据值的最大值和最小值的平均数。
例题7：有如下9个数，65，81，73，85，94，79，67，83，82。求中程数。
解析：max=94，min=65，中程数=（94+65）/2=79.5
◇中位数：
又称中点数，中值。中数是按顺序排列的一组数据中居于中间位置的数，即在这组数据中，有一半的数据比他大，有一半的数据比他小，这里用m0.5来表示中位数。当n为奇数时，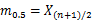
；当n为偶数时，
。在EXCEL中，可以用MEDIAN函数。
例题8：有如下8个数：20，21，23，23，25，29，32，33。求中位数。
解析：8个数，在（n+1）/2=4.5位置，即第四个和第五个的平均数。
故，median=(23+25)/2=24。
当测试数据的数量很大时，中位数的计算开销很大。然而，对于数值属性，我们可以很容易计算中位数的近似值。中位数近似值公式：
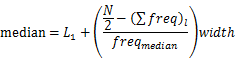
其中：
L1：中位数区间的下限
N：数据集数据个数
(∑freq)l：低于中位数区间的所有区间的频数和
freqmedian：中位数区间的频数
width：中位数区域的宽度
例题9：假定给定的数据集的值已经分组为区间，区间和对应的频数如下：
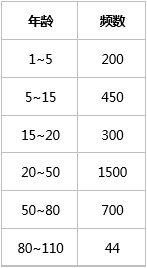
解析：
1）先判断中位数所在区间。N=200+450+300+1500+700+44=3194。样本数据总量为3194，一半为N/2=1597。因为200+450+300=950；200+450+300+1500=2450。所以中位数所在区间为：950~2450，即20~50岁。
2）计算近似中位数参数。
L1=20 中位数区间的下限
N/2=1597 样本数据量的一半
(∑freq)l=950 低于中位数区间的所有区间的频数和
freqmedian=1500 中位数区间的频数。
width=30 中位数区域的宽度。
3）计算近似中位数。Median=20+(1597-950)/1500*30=32.94 (岁)
