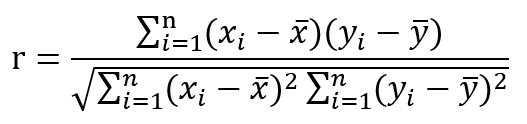1、利用帕累托法则分析主要矛盾和次要矛盾，培养学生看清事物本质，抓住事物的核心去做事情。
2、利用学生自己的学习数据，进行周期性分析，分析每个学生的学习状态。
对数据进行质量分析后，接下来可以通过绘制图表、计算某些特征量等手段进行数据的特征分析，通常特征分析包括对比分析、贡献度分析、周期性分析、相关分析、分布分析和统计分析等。
（1）对比分析
对比分析时之把两个相互联系的指标进行比较，从数量上展示和说明研究对象规模的大小、水平的高低、速度的快慢、以及各种关系是否协调。特别适用于指标间的横纵向比较、时间序列的比较分析。在对比分析中，选择合适的对比标准是十分关键的步骤，选择合适才能作出客观的评价，选择不合适，评价可能会得出错误的结论。
对比分析有两种形式：一是绝对数对比；另一个是相对数对比。
（2）贡献度分析
贡献度分析又称帕累托分析，它的原理是帕累托法则，又称为20/80定律。同样的投入放在不同的地方会产生不同的效益。比如，对于一个公司来说，80%的利润常常来自于20%的最畅销的产品，而其他80%的产品只产生了20%的利润。
（3）周期性分析
周期性分析是探索某个变量是否随着时间变化而呈现出某种周期变化的趋势。时间尺度相对较长的趋势有年度周期性趋势、季节周期性趋势、相对较短的有月度周期性趋势、周度周期性趋势，甚至更短的天、小时周期性趋势。
（4）相关分析
分析连续变量之间线性相关程度的强弱，并用适度的统计指标表示出来的过程称为相关分析。
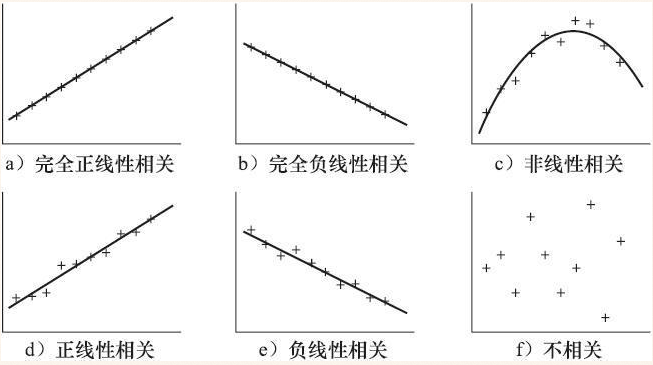
◇直接绘制散点图
判断两个变量是否具有线性相关的最直观的方法就是绘制散点图，如下图所示。
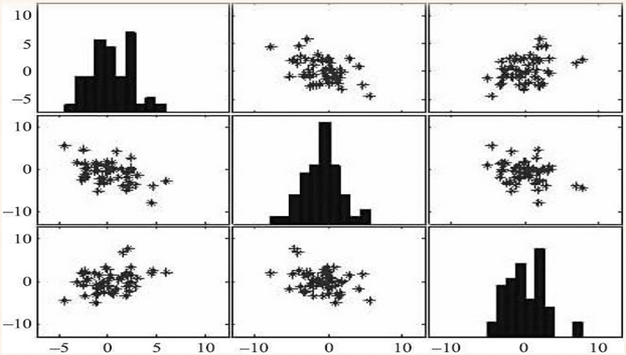
◇绘制散点图矩阵
需要同时考虑多个变量间的相关关系时，一一绘制其简单散点图会是非麻烦。此时可利用散点图矩阵来同时绘制各变量间的散点图，从而快速发现多个变量间的主要相关性，这在进行多元线性回归时显得尤为重要。
◇计算相关系数
Pearson相关系数，一般用于分析两个连续变量之间的关系，其计算公式如下：
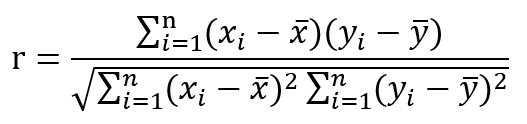
r 的取值范围在-1和1之间。当r > 0 时为正相关，r<0时为负相关。
|r|=1，表示完全线性相关，即函数关系
|r|=0，表示不存在线性相关关系
|r|≤0.3 为不存在线性相关
0.3<|r|≤0.5 为低度线性相关
0.5<|r|≤0.8 为显著线性相关
|r|>0.8 为高度线性相关
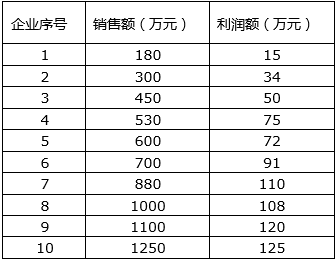
示例1：皮尔逊相关分析
一个企业的产品销售额与利润之间呈现出同方向变化的关系，也就是利润随着销售额的增加而增加，反之亦然。如下图所示。请你判断产品销售额和利润是否相关？
解析：
方法1：用皮尔逊相关系数公式直接计算。
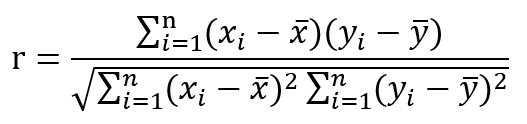
其中，n=10；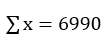
；
；
；
；
；
；
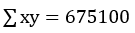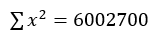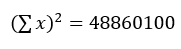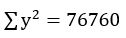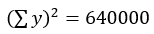；计算得r=0.9709
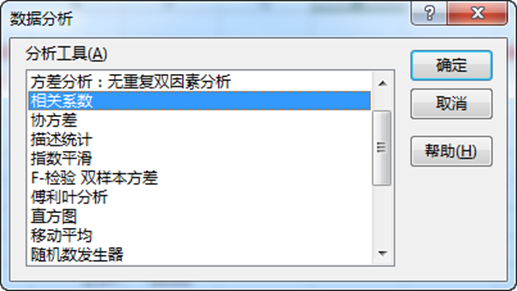
方法2：EXCEL中直接用CORREL函数
方法3：用EXCEL分析工具，如下图：
