数据质量分析是数据挖掘中数据准备过程的重要一环,是数据预处理的前提,也是数据挖掘分析结论有效性和准确性的基础,没有可信的数据,数据挖掘构建的模型将是空中楼阁。
数据质量分析的主要任务是检查原始数据中是否存在脏数据、脏数据一般是指不符合要求,以及不能直接进行相应分析的数据。在日常的数据挖掘工作中,脏数据包括:
◇ 缺失值
◇ 异常值
◇ 不一致的值
◇ 重复数据及含有特殊符号(如#、¥、*)的数据
(1)缺失值分析
数据的却是主要包括记录的缺失和记录中某个字段信息的缺失,两者都会造成分析结果的不准确。以下从缺失值产生的原因及影响等方面展开分析。
缺失值产生的原因
◇ 有些信息暂时无法获取,或者获取信息的代价太大
◇ 有些信息是被遗漏的,可能是因为输入时认为不重要、忘记填写或对数据理解错误等一些人为因素而造成的,也可能是由于数据采集设备的故障、存储介质的故障、传输媒体的故障等非人为原因而丢失的。
◇ 属性值不存在。在某些情况下,缺失值并不意味着数据有错误。对于一些对象来说某些属性值是不存在的,如一个未婚者的配偶姓名、一个无业者的固定收入等。

(2)异常值分析
异常值分析时检验数据是否有录入错误以及含有不合常理的数据。忽视异常值的存在是十分危险的,不加以剔除,会对分析结果带来不良的影响。
异常值是指样本中的个别值,其数值明显偏离其余的观测值。异常值也称为离群点,异常值的分析也称为离群点分析。常用以下三种方法:
◇ 简单统计量分析
可以先对变量做一个描述性统计,进而查看哪些数据是不合理的。最常用的统计量是最大值和最小值,用来判断这个变量的取值是否超出了合理的范围。如客户的年龄最大值为199岁,则该变量的取值存在着异常。
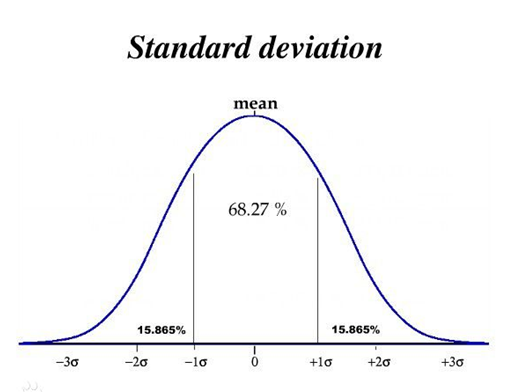
◇ 3σ原则
如果数据服从正态分布,在3σ原则下,异常值被定义为一组测定值中与平均值的偏差超过三倍标准差的值。在正态分布的假设下,距离平均值3σ之外的值出现的概率为极个别的小概率事件。
如果数据不服从正态分布,也可以用远离平均值的多少倍的标准差来描述。
◇ 箱形图分析
箱形图又称为盒须图、盒式图或箱线图,是一种用作显示一组数据分散情况资料的统计图。因形状如箱子而得名。在各种领域也经常被使用,常见于品质管理。
在一组观测数据中,Q1称为第一分位数,或下四分位数,表示全部观测值中有四分之一的数据取值比它小;Q2称为中位数,表示位置中位数,如果数据量个数为奇数,则中位数为位置中间的数,如果数据量个数为偶数,则中位数为位置中间的两个数的平均值。Q3称为第三份位数,或上四分位数,表示全部观测值中有四分之三的数据比它小。R=Q3-Q1的值被称为内距。表示中间50%的数据。
箱形图提供了识别异常值的一个标准,异常值通常被定义为小于Q1-1.5R或大于Q3+1.5R的值。

箱线图的绘制方法是:先找出一组数据的最大值、最小值、中位数和两个四分位数;然后, 连接两个四分位数画出箱子;再将最大值和最小值与箱子相连接,中位数在箱子中间。
四分位数位置的确定方法:
Q1的位置= (n+1) × 0.25
Q2的位置= (n+1) × 0.5
Q3的位置= (n+1) × 0.75
n表示项数
对于四分位数的确定,有不同的方法,另外一种方法基于N-1 基础。即
Q1的位置=1+(n-1)x 0.25
Q2的位置=1+(n-1)x 0.5
Q3的位置=1+(n-1)x 0.75
Excel 中有两个四分位数的函数。QUARTILE.EXC和QUARTILE.INC
QUARTILE.EXC 基于 N+1 的方法,QUARTILE.INC基于N-1的方法。
示例1:现有如下的观测数据:14,6,3,2,4,15,11,8,-14,7,2,-8,3,4,10,28,25。请你用箱形图方法判断异常点。
解析:
样本个数:n=17。min=-14,max=28。EXCEL中可以用count、min、max函数实现。
(1)将原数据进行排序,排序后的数据为:-14,-8,2,2,3,3,4,4,6,7,8,10,11,14,15,25,28。
(2)中位数(Q2):50%位置,n=17,故在(n+1)/2=9,第九个数是6。EXCEL中可以用median函数实现。
(3)第一分位数(Q1):25%位置,n=17,故在(n+1)/4=4.5,第4个数和第5个数的平均值,即(2+3)/2=2.5。EXCEL中可以用QUARTILE函数、或PERCENTILE函数实现。
(4)第三份位数(Q3):75%位置,n=17,故在3*(n+1)/4=13.5,第13个数和第14个数的平均值,即(11+14)/2=12.5。EXCEL中可以用QUARTILE函数、或PERCENTILE函数实现。
(5)内距(R):R=Q3-Q1=10
(6)Whisker上限(理论值):Q3+1.5*R=12.5+1.5*10=27.5
(7)Whisker下限(理论值):Q1-1.5*R=2.5-1.5*10=-12.5
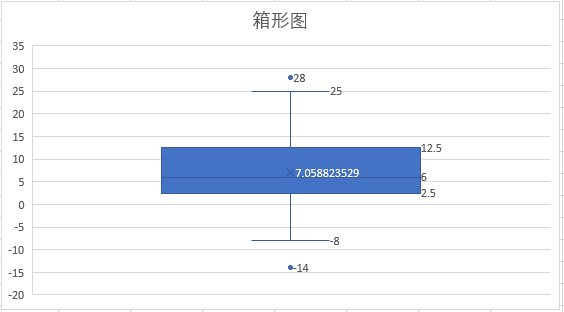
(8)Whisker上限(实际值):25(小于理论值的最大实际值)
(9)Whisker下限(实际值):-8(大于理论值的最小实际值)
(10)异常点:-14和28
EXCEL2016版本以上绘制的箱形图如下:
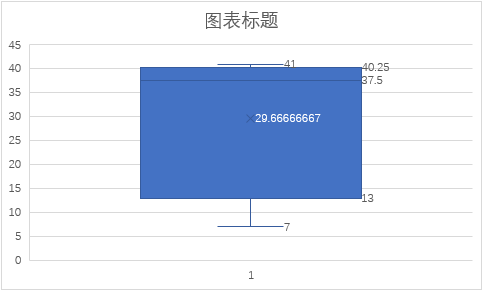
示例2:现有如下的观测数据:7, 15, 36, 39, 40, 41,请你用箱形图方法判断异常点。
解析:样本个数:n=6。min=7,max=41。
(1)中位数(Q2):50%位置,n=6,故在(n+1)/2=3.5,第3和第4位置上的数的平均值,即Q2=(36+39)/2=37.5。
(3)第一分位数(Q1):25%位置,n=6,故在(n+1)/4=1.75,Q1在第1个数和第2个数之间,且靠近第2个数,即Q1=7*0.25+15*0.75=13。
(4)第三份位数(Q3):75%位置,n=6,故在3*(n+1)/4=5.25,Q2在第5个数和第6个数之间,且靠近第5个数,即Q3=40*0.75+41*0.25=40.25。
(5)内距(R):R=Q3-Q1=27.25
(6)Whisker上限(理论值):Q3+1.5*R=40.25+1.5*27.25=81.125
(7)Whisker下限(理论值):Q1-1.5*R=13-1.5*27.25=-27.875
(8)Whisker上限(实际值):41(小于理论值的最大实际值)
(9)Whisker下限(实际值):7(大于理论值的最小实际值)
(10)异常点:无