计算思维导论

吕橙

目录

  • 1 从这里开始你的学习
    • 1.1 欢迎词
    • 1.2 单元学习目标
    • 1.3 课程学习说明
      • 1.3.1 课程概述与内容
      • 1.3.2 学习目标
      • 1.3.3 学习安排
      • 1.3.4 学习活动
      • 1.3.5 考核标准
      • 1.3.6 学习准则
    • 1.4 先修知识与必备技能
      • 1.4.1 学习平台使用及技术支持
      • 1.4.2 必备基础要求
      • 1.4.3 学习资源使用指南
      • 1.4.4 教材电子版下载
      • 1.4.5 相关软件下载与安装方法
      • 1.4.6 答疑安排与教师课表
      • 1.4.7 作业和考试反馈
    • 1.5 FAQ：常见问题解答
    • 1.6 教师自我介绍和学生自我介绍
    • 1.7 计算思维能力调查
    • 1.8 学习风格调查
    • 1.9 交流协作分组情况
    • 1.10 第0讲 单元测试
  • 2 计算思维概述——第1周
    • 2.1 单元学习目标
    • 2.2 本章课件下载
    • 2.3 课程思政
      • 2.3.1 线上思政（自主学习）
      • 2.3.2 线下课程思政
    • 2.4 计算无所不在
    • 2.5 计算思维概述
    • 2.6 计算工具与计算机
    • 2.7 第1讲 单元测试
    • 2.8 上机实验1-1：计算思维概述——系统自动评阅
    • 2.9 延伸学习
  • 3 计算基础——第2~3周
    • 3.1 单元学习目标
    • 3.2 本章课件下载
    • 3.3 课程思政
      • 3.3.1 线上课程思政（自主学习）
      • 3.3.2 线下课程思政
    • 3.4 初识二进制
    • 3.5 二进制的运算（自主学习）
    • 3.6 数制转换
    • 3.7 数的表示
    • 3.8 字符编码
    • 3.9 声音图像编码（自主学习）
    • 3.10 第2讲 单元测试
    • 3.11 上机实验2-1：进制转换——系统自动评阅
    • 3.12 延伸学习
  • 4 计算平台——第4周
    • 4.1 单元学习目标
    • 4.2 本章课件下载
    • 4.3 课程思政
      • 4.3.1 线上课程思政（自主学习）
      • 4.3.2 线下课程思政
    • 4.4 计算机系统
    • 4.5 硬件之主板（自主学习）
    • 4.6 硬件之接口与总线（自主学习）
    • 4.7 硬件之CPU（自主学习）
    • 4.8 硬件之内存（自主学习）
    • 4.9 硬件之外存（自主学习）
    • 4.10 硬件之输入输出设备（自主学习）
    • 4.11 计算机基本工作原理
    • 4.12 操作系统之处理机功能
    • 4.13 操作系统之其他功能
    • 4.14 第3讲 单元测试
    • 4.15 上机实验3-1：计算机硬件系统——系统自动评阅
    • 4.16 延伸学习
  • 5 问题求解——第5~7周
    • 5.1 单元学习目标
    • 5.2 本章课件下载
    • 5.3 课程导图与设计
    • 5.4 典型课例（课堂实录）
    • 5.5 线上思政（自主学习）
    • 5.6 线下思政
    • 5.7 纸版教材在线阅读
    • 5.8 什么是问题求解？
    • 5.9 算法与算法描述
    • 5.10 顺序结构
    • 5.11 选择结构
    • 5.12 循环结构
    • 5.13 算法策略基础之数组
    • 5.14 算法策略基础之函数
    • 5.15 算法策略之枚举法
    • 5.16 算法策略之递归法
    • 5.17 算法策略之递推法
    • 5.18 算法策略之迭代法
    • 5.19 算法策略之分治法（自主学习）
    • 5.20 算法策略之动态规划（自主学习）
    • 5.21 算法策略之贪心算法（自主学习）
    • 5.22 算法策略之回溯法（自主学习）
    • 5.23 算法策略之查找
    • 5.24 算法策略之排序
    • 5.25 实验4-1：Raptor 软件基本操作（教师手工评阅）
    • 5.26 实验4-2：算法设计与分析（生生互评）
    • 5.27 实验4-3：问题求解（自主学习）
    • 5.28 实验7-1：解题报告
    • 5.29 实验7-2：解题报告
    • 5.30 实验7-3：解题报告（自主学习）
    • 5.31 第7讲 单元测试
    • 5.32 延伸学习
  • 6 网络技术与信息共享——第8周
    • 6.1 单元学习目标
    • 6.2 本章课件下载
    • 6.3 课程思政
      • 6.3.1 线上思政（自主学习）
      • 6.3.2 线下思政
    • 6.4 初识网络
    • 6.5 网络分类（自主学习）
    • 6.6 网络体系结构
    • 6.7 网络设备（自主学习）
    • 6.8 局域网的搭建（自主学习）
    • 6.9 IP与域名系统
    • 6.10 划分子网
    • 6.11 Internet 服务（自主学习）
    • 6.12 数字公民与网络安全（自主学习）
    • 6.13 组网实例（自主学习）
    • 6.14 第4讲 单元测试
    • 6.15 上机实验4（PBL）：网络互联训练——生生互评
      • 6.15.1 思科网络实验室1：网络布线
      • 6.15.2 思科网络实验室2：将计算机添加到现有网络
      • 6.15.3 思科网络实验室3：连接无线路由器
      • 6.15.4 思科网络实验室4：测试无线连接
    • 6.16 延伸学习
  • 7 数据库技术与数据管理——第9-10周
    • 7.1 单元学习目标
    • 7.2 本章课件下载
    • 7.3 课程思政
      • 7.3.1 线上思政（自主学习）
      • 7.3.2 线下思政
    • 7.4 数据库基本概念（自主学习）
    • 7.5 数据库的设计方法
    • 7.6 数据库的规范化设计1
    • 7.7 数据库的规范化设计2
    • 7.8 Access数据库的创建与查询（自主学习）
    • 7.9 关系代数理论
    • 7.10 SQL语句编程（自主学习）
    • 7.11 实验5-1：数据库设计——互评作业
    • 7.12 实验5-2：窗体与报表——互评作业
    • 7.13 第5讲 单元测试
    • 7.14 延伸学习
  • 8 逻辑思维——第10-11周
    • 8.1 单元学习目标
    • 8.2 本章课件下载
    • 8.3 课程导图与设计
    • 8.4 典型课例（课堂实录）
    • 8.5 线上思政（自主学习）
    • 8.6 线下思政
    • 8.7 实验6-1：逻辑推理（PBL个人项目——教师手工评阅）
    • 8.8 前6章思维导图训练（PBL小组项目——互评）
    • 8.9 纸版教材在线阅读
    • 8.10 逻辑思维及其训练方法（自主学习）
    • 8.11 命题与命题判断
    • 8.12 命题符号化
    • 8.13 布尔代数与真值表
    • 8.14 命题演算与逻辑推理
    • 8.15 习题课
    • 8.16 实验6-1：解题报告
    • 8.17 第6讲 单元测试
    • 8.18 延伸学习
  • 9 数据分析与数据挖掘——第11~12周
    • 9.1 单元学习目标
    • 9.2 本章课件下载
    • 9.3 课程导图与设计
    • 9.4 课程思政
    • 9.5 线上思政（自主学习）
    • 9.6 线下思政
    • 9.7 上机实验8-1：数据分析（PBL个人项目——系统自动评阅）
    • 9.8 上机实验8-2：数据挖掘（自主学习）
    • 9.9 纸版教材在线阅读
    • 9.10 数据挖掘概述（自主学习）
    • 9.11 数据采集（自主学习）
    • 9.12 数据探索之数据质量分析
    • 9.13 数据探索之数据特征分析
    • 9.14 数据特征分析之分布分析
    • 9.15 数据特征分析之集中统计分析
    • 9.16 数据特征分析之离散统计分析
    • 9.17 数据预处理
    • 9.18 分类
    • 9.19 预测
    • 9.20 聚类分析（自主学习）
    • 9.21 关联规则（自主学习）
    • 9.22 第8讲 单元测试
    • 9.23 延伸学习
  • 10 课程思政案例篇
    • 10.1 课程思政案例
  • 11 特色思维训练库
    • 11.1 数学思维（50篇）
    • 11.2 逻辑思维（50篇）
    • 11.3 AI智能思维（50篇）
    • 11.4 专业思维（50篇）
  • 12 游戏编程案例篇
    • 12.1 编程游戏关卡（30篇）
    • 12.2 编程游戏制作（10关）
  • 13 大工程思训项目库
    • 13.1 综合性案例——北京冬奥会智能餐厅设计
    • 13.2 综合性案例——北京冬奥会运动员密码设置
    • 13.3 综合性案例——北京冬奥电脑装配
    • 13.4 综合性案例——北京冬奥网络安全培训
    • 13.5 综合性案例——北京冬奥会商品销售数据库系统设计
    • 13.6 综合性案例——北京冬奥金牌榜预测
    • 13.7 综合性案例——北京冬奥会奖牌榜自动更新算法设计
    • 13.8 综合性案例——北京冬奥会线上销售大数据分析
  • 14 考试专栏
    • 14.1 教材及教材修订
    • 14.2 考试纪律
    • 14.3 考试注意事项
    • 14.4 逻辑符号的录入方法
    • 14.5 期末考试模拟样卷
第6讲 单元测试
  • 1 知识点回顾
  • 2 练习题及解析
  • 3 章节自测

谈到逻辑，并不陌生，我们可能马上就会想到幽默，让我们先来看一段刘宝瑞和郭启儒的相声《蛤蟆鼓》：

甲：你这么有学问，我请问你，蛤蟆那么点小，叫声为什么那么大?

乙：蛤蟆叫声大，是因为嘴大，脖子又憨。凡是嘴大脖子憨的叫声都大。

甲：我家的字纸篓也是嘴大脖子憨，怎么不响呢?

乙：那它是竹子编的，竹子编的它都不响。

甲：和尚吹的那个笙管也是竹子编的，它怎么就响呢?

……

甲：有胶性的，胶鞋底为什么不响呢?

乙：那它挨着地了，不响。

甲：挨着地的三轮车胎，放起炮来怎么又那么响?

乙：什么乱七八糟的!……

上述回答中，每个细节都是很认真的，似乎都说明了一种道理，但经不起推敲，这段相声之所以如此引人捧腹，是因为幽默往往是有逻辑框架的，同时也是符合逻辑的，两种逻辑间的交错点就是幽默。

或许我们还会想到言辞犀利、逻辑严谨的大学生辩论会，想到才华横溢、思维敏捷的推理大师福尔摩斯，这些都和逻辑思维密不可分。

逻辑学：就是关于思维的逻辑形式及其规律的科学。它作为一门科学的逻辑，是既古老又年轻的。历史悠久，源远流长。它有三大源泉：古希腊的形式逻辑，中国先秦的名辩逻辑，古印度的因明。

逻辑思维，或称抽象思维，垂直思维，是人们在认识过程中借助于概念、命题、判断和推理等形式，运用分析、综合、归纳和演绎等方法，对丰富多彩的感性事物进行去粗取精、去伪存真、由此及彼、由表及里的加工制作以反映现实的过程。

逻辑思维的特征有：（1）概念的特征：内涵和外延。（2）判断的特征：一是判断必须对事物有所断定；二是判断总有真假。（3）推理的特征：演绎推理的逻辑特征是：如果前提真，那么结论一定真，是必然性推理；非演绎推理的逻辑特征是：虽然前提是真的，但不能保证结论是真的，是或然性推理。

逻辑思维常见的训练方法主要有：

（1）概念训练：如白马非马论。

（2）推理训练：如推理小说《血字的研究》。

（3）类比训练：如贝都印人的推断。

（4）三段论训练：如大前提：法律都是有阶级性的。小前提：刑法是法律。结论：刑法是有阶级性的。

（5）演绎训练法：如谁说谎？

（6）归纳训练：如完全归纳和不完全归纳

（7）分析训练：如翻硬币。

命题是描述事件的，一个命题所描述的如果符合事实，它就是真的，如果不符合事实，它就是假的。因此，一个语句表达命题则它或者是真的或者是假的，无所谓真假的语句不表达命题。例如语句“张三当时在案发现场吗？”是一个疑问，它表达的是对某情况的疑问，无所谓真假，因此我们说它不表达命题。而语句“张三当时在案发现场。”是一个陈述句，它所陈述的若符合事实它就是真的，否则就是假的。因此该语句表达一个命题。一般来就，只有陈述句才有真假，因此只有陈述句表达命题。

悖论是表面上同一命题或推理中隐含着两个对立的结论，而这两个结论都能自圆其说。悖论的抽象公式就是：如果事件A发生，则推导出非A，非A发生则推导出A。

命题用符号表示称为命题符号化。通常用大写的带或不带下标的英文字母表示命题。如：A、B、C、...P、Q、R、... Ai、Bi 、Ci、...Pi、Qi、...

命题演算是通过逻辑联结词，由简单命题构成更复杂的命题（复合命题）。

定义1：令P为一命题，则P的否定表示为￢P，指“不是P所说的情形”。命题￢P读作“非P”。￢P的真值和P的真值相反。

定义2：令P和Q为命题，P，Q的合取用P∧Q表示，即命题“P并且Q”。当P和Q都是真时，P∧Q命题为真，否则为假。

定义3：令P和Q为命题，P，Q的析取用P∨Q表示，即命题“P或Q”。当P和Q均为假时，P∨Q命题为假，否则为真。

定义4：令P和Q为命题，P，Q的异或用P⊕Q表示，即命题“P异或Q”。当P和Q中只有一个为真时，P⊕Q命题为真，否则为假。

定义5：令P和Q为命题，条件语句P→Q是命题，“若P，则Q”。当P为真而Q为假时，条件语句P→Q为假，否则为真。在条件语句P→Q中，P称为假设（或前项、前提），Q称为结论（或推论）。条件语句也称为蕴含。

定义6：令P和Q为命题，双条件语句PQ是命题，“P当且仅当Q”。当P和Q有同样的真值时，双条件语句为真，否则为假。双条件语句也称为双蕴含、等价。

逻辑联结词的优先级为：括号→否定→合取→析取→蕴含→等价

含有n个命题变项的公式A共有2^个取值。将公式A在所有赋值之下取值情况列成表，称为A的真值表。

真值表的构造步骤如下：

（1）找出公式中所含的命题变项，列出所有可能的取值。

（2）按低到高的顺序写出各层次。

（3）对应各取值，计算公式各层次的值，直到计算出公式的值。

由已知等式推演出另外一些等值式的过程称为等值演算。

设A为一个命题公式，命题在各种赋值情况下取值均为真，则称A为永真式或重言式。

设A为一个命题公式，命题在各种赋值情况下取值均为假，则称A为矛盾式或永假式。

设A，B为两个命题公式，若等价式AB为永真式（重言式），则称A为B是等值的（或逻辑等价），记作A⇔B

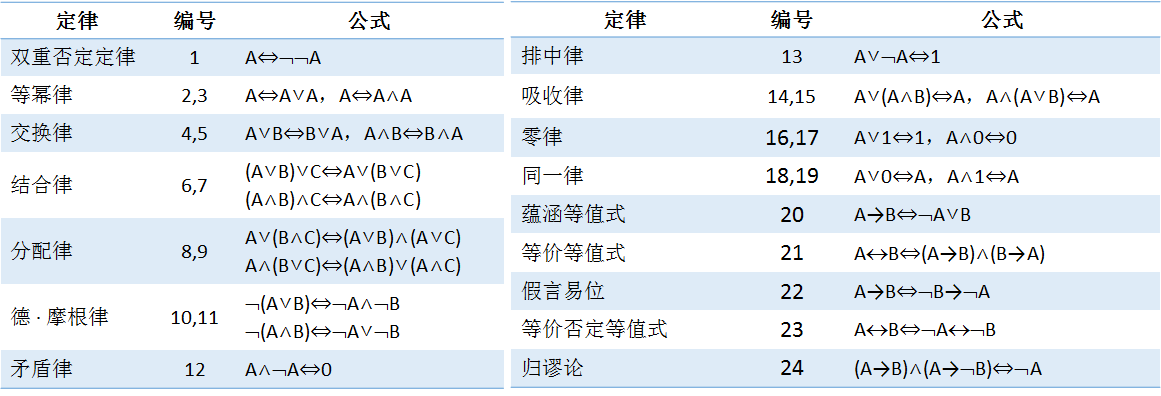
逻辑推理的方法：（1）真值表法、（2）等值演算法、（3）构造证明法（反证法）

示例：有三个医生都说Robert是他们的兄弟，甲说乙说谎，乙说丙说谎，丙说甲乙都说谎，已知三人中，有一人说真话，问谁在说谎？

分析：

设 p：甲说真话、q：乙说真话、r：丙说真话

（1）命题符号化

甲说：￢q

乙说：￢r

丙说：￢p∧￢q

（2）真值表：￢q+￢r+(￢p∧￢q)=1

p
qr￢p￢q￢r￢p∧￢q真话数
00111012
01010101
1
0001102

结论：q=1，即乙说真话。