

19世纪早期,英国数学家乔治·布尔(George Boole,1815-1864)突发奇想:人的思想能不能用数学表达?
此前,数学只用于计算,没有人意识到,数学还能表达人的逻辑思维。

两千年来,哲学书都是用文字写的。比如,最著名的三段论:
所有人都是要死的,
苏格拉底是人,
所以,苏格拉底是要死的。
乔治·布尔认为,这种推理可以用数学表达,也就是说,哲学书完全可以用数学写。这就是数理逻辑的起源。

乔治·布尔发明的工具,叫做"集合论"(Set theory)。他认为,逻辑思维的基础是一个个集合(Set),每一个命题表达的都是集合之间的关系。

交集可以用逻辑与(and)、逻辑乘(X)、或点积(●)表示;
并集可以用逻辑或(or)、逻辑加(+)表示。
差集可以用逻辑非(not)、逻辑减(-)、逻辑反(¬)表示。
异或可以用逻辑异或(Xor、⊕)表示。
比如,所有人类组成一个集合R,所有会死的东西组成一个集合D。
所有人都是要死的
集合论的写法就是:R X D = R
上面这个式子的意思是,R与D的交集就是R。
同样的,苏格拉底也是一个集合S,这个集合里面只有苏格拉底一个成员。
苏格拉底是人
// 等同于
S X R = S
上面式子的意思是,苏格拉底与人类的交集,就是苏格拉底。
将第一个式子代入第二个式子,就得到了结论。
S X (R X D)
= (S X R) X D
= S X D
= S
这个式子的意思是,苏格拉底与会死的东西的交集,就是苏格拉底,即苏格拉底也属于会死的东西。

前面的三段论比较容易,一眼就能看出结论。但是,有些三段轮比较复杂,不容易立即反应过来。
请看下面这两句话。
"鸭嘴兽是卵生的哺乳动物。鸭嘴兽是澳洲的动物。"
你能一眼得到结论吗?
鸭嘴兽 X 卵生 = 鸭嘴兽
鸭嘴兽 x 澳洲 = 鸭嘴兽
将第一个式子代入第二个,就会得到:
鸭嘴兽 X 卵生 x 澳洲 = 鸭嘴兽
// 相当于
卵生 x 澳洲 = 鸭嘴兽 + 其他
因此,结论就是"有的卵生动物是澳洲的动物",或者"有的澳洲的动物是卵生动物"。
由此可见,集合论可以帮助我们得到直觉无法得到的结论,保证推理过程正确,比文字推导更可靠。

既然命题可以用集合论表达,那么逻辑推导无非就是一系列集合运算。
由于集合运算的结果还是集合,那么通过判断个体是否属于指定集合,就可以计算命题的真伪。
一名顾客走进宠物店,对店员说:"我想要一只公猫,白色或黄色均可;或者一只母猫,除了白色,其他颜色均可;或者只要是黑猫,我也要。"
这名顾客的要求用集合论表达,就是下面的式子。
公猫 X (白色 + 黄色)
+ 母猫 X 非白色
+ 黑猫
店员拿出一只灰色的公猫,请问是否满足要求?
布尔代数规定,个体属于某个集合用1表示,不属于就用0表示。 灰色的公猫属于公猫集合,就是1,不属于白色集合,就是0。
上面的表达式变成下面这样。
1 X (0 + 0)
+ 0 X 1
+ 0
= 0
因此,就得到结论,灰色的公猫不满足要求。
这就是布尔代数:计算命题真伪的数学方法。

布尔代数的运算法则与集合论很像。
交集的运算法则如下:
1 X 1 = 1
1 X 0 = 0
0 X 0 = 0
并集的运算法则如下:
1 + 1 = 1
1 + 0 = 1
0 + 0 = 0
集合论可以描述逻辑推理过程,布尔代数可以判断某个命题是否符合这个过程。人类的推理和判断,因此就变成了数学运算。
20 世纪初,英国科学家香农指出,布尔代数可以用来描述电路,或者说,电路可以模拟布尔代数。于是,人类的推理和判断,就可以用电路实现了。这就是计算机的实现基础。
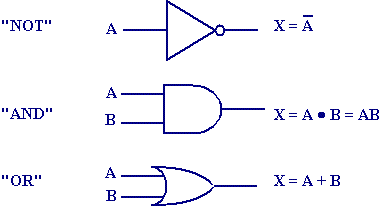

布尔运算符,又称为逻辑运算符,主要有与、或、非、异或。
运算符 | 符号 | 作用 |
与 | ● × and | 称为逻辑与,只有两个操作数都是true,结果才为true |
或 | + or | 称为逻辑或,如果一个操作数或多个操作数为true,则逻辑或运算符返回布尔值true;只有全部操作数为false,结果才为false |
非 | - ¬ not | 称为逻辑非,就是指本来值的反值。 |
异或 | ⊕ Xor | 称为逻辑异或,如果a、b两个值不同,则异或结果为1,如果a、b两个值相同,异或结果为0 |
布尔运算规则:与、或、异或是双目运算
| a | b | and | or | xor |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
1
| 1 | 1 | 1 | 0 |
非运算是单目运算

含有n个命题变项的公式A共有2^个取值。将公式A在所有赋值之下取值情况列成表,称为A的真值表。
构造步骤:
⑴ 找出公式中所含的命题变项,并列出所有可能的取值。
⑵ 按低到高的顺序写出各层次。
⑶ 对应各取值,计算公式各层次的值,直到计算出公式的值。
例如,求命题公式 (p∧¬q)→r 的真值表
⑴ 找出公式中所含的命题变项,并列出所有可能的取值。公式中变项有三项分别是p、q、r。
⑵ 按低到高的顺序写出各层次。三项,共8种可能情况。
⑶ 对应各取值,计算公式各层次的值,直到计算出公式的值。
p
| q | r
| ¬q | p∧¬q | (p∧¬q)→r |
| 0 | 0 | 0 | 1 | 0
| 1 |
| 0 | 0 | 1 | 1
| 0 | 1 |
| 0 | 1 | 0 | 0
| 0 | 1 |
| 0 | 1 | 1 | 0
| 0 | 1 |
1
| 0 | 0 | 1
| 1 | 0 |
1
| 0 | 1 | 1
| 1 | 1 |
| 1 | 1 | 0 | 0
| 0 | 1 |
1
| 1 | 1 | 0
| 0 | 1 |


















