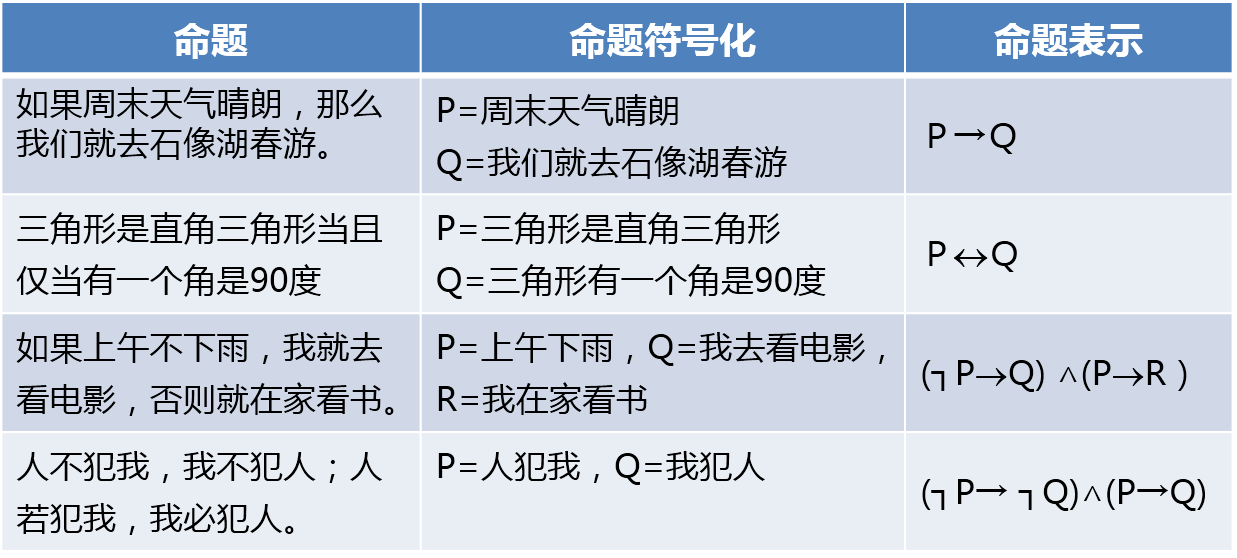
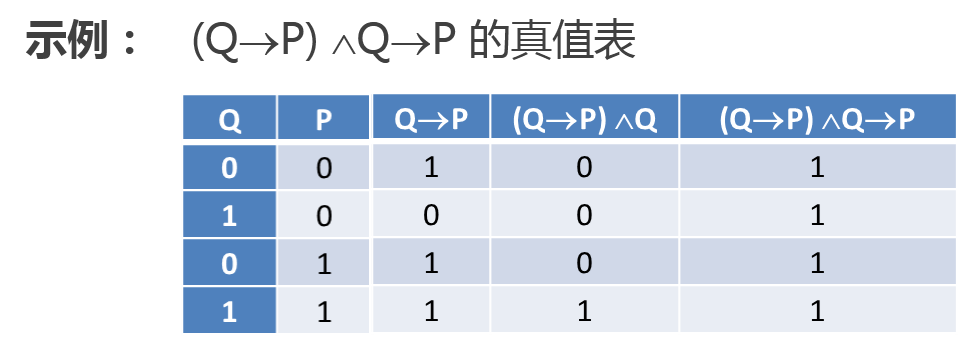
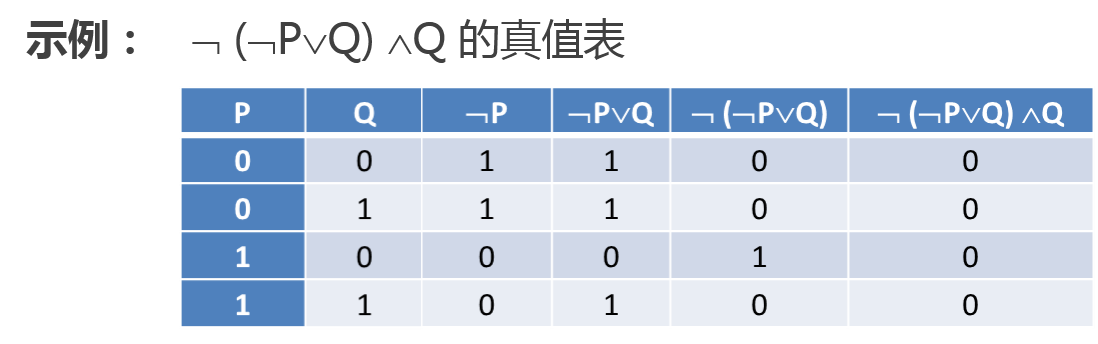
◇ 命题符号化：命题用符号表示称为命题符号化。
◇ 表示方法：通常用大写的带或不带下标的英文字母表示命题。如：A、B、C、...P、Q、R、... Ai、Bi 、Ci、...Pi、Qi、...
◇ 命题标识符：表示命题的符号称为命题标识符。
◇ 命题常量：一个命题标识符如表示确定的命题，就称为命题常量。
◇ 命题变元：如果命题标识符只表示任意命题的位置标志，就称为命题变元。
◇ 逻辑联结词：命题演算是通过逻辑联结词，由简单命题构成更复杂的命题（复合命题）。逻辑连接词类似于运算符号。
◇ 联结词种类：否定、合取、析取、蕴涵、等价。
（1）否定
设P为一命题，P的否定是一个新的命题，记作￢P。若P为True，￢P为False；若P为False，￢P为True。
自然语言：非、不、并非。
例如，设P：今天下雨。￢P: 今天不下雨。
（2）合取
两个命题P和Q的合取是一个复合命题，记作P∧Q。当且仅当P，Q同时为True时，P∧Q为True。在其他情况下，P∧Q的真值为False。
自然语言：和、与、并且、既...又...、不仅...而且...、虽然...但是...。
例如，设P：3是素数；Q：3是奇数。则，P∧Q：3既是素数又是奇数。
（3）析取
两个命题P和Q的析取是一个复合命题，记作P∨Q。当且仅当P，同时为False时，P∨Q的真值为False，否则PVQ的真值为True。
自然语言：或、或者。
或包含相容或和相异或两种。例如，灯泡或开关故障；第一节课上数学课或英语课。
仔细分析两处的或有所不同，灯泡故障和开关故障可以同时发生，而第一节课上数学，上英语不可以同时发生。故此，
相容或：设P：灯泡故障，Q：开关故障。灯泡或开关故障（可能同时发生）为 P∨Q。
相异或：设P：第一节课上数学课，Q：第一节课上英语课。第一节课上数学课或英语课为 (P∧￢Q)∨(￢P∧Q)。
（4）蕴含（蕴涵）
给定两个命题P和Q，其条件命题是一个复合命题，记作P→Q，当且仅当P的真值为True，Q的真值为False时，P→Q的真值为False，否则P→Q的真值为True。
自然语言："如果…，那么…"、"若…，则…"、"只要……，就……"
例如，P：周末天气晴朗；Q：我们将到郊外旅游。P→Q：如果周末天气晴朗，则我们将郊外旅游。
P→Q它表示自然语言的“如果…，则…”这种假言判断的，如果P为真命题，Q也为真命题时，P→Q是真命题，当P为真命题，而Q为假命题时，P→Q是一个假命题。比如张三说，“如果明天天不下雨(P)，那么他去你家玩(Q)”，如果第二天天不下雨，他去了你家，他说了真话(P→Q为真)，如果天不下雨，但他没有去你家，显然他说了谎话（此时P→Q为假）。
但是当P为假时，无论此时Q是真命题还是假命题，P→Q的真假好象无法判断，又如第二天天下雨了，无论此时张三去不去你家，无法判断张三说的话的真伪，但是他并没有食言，从这种意义上说，张三说的话仍为真，这称为“善意推定”。
因此我们规定，将P为假这种情况一律规定P→Q为真，例如命题“如果2+3=4，则太阳从东边出来”，“如果2+3=4，则太阳从西边出来”，均认为是真命题。
另外，对P→Q的判断，P和Q可以没有因果关系，或者说前提或结论。比如2+3是否等于4，其实和太阳是从东边出来还是西边出来没有啥关系。并不是说 2+3=4 是前提，太阳从东边出来是结论。
思考：
◇ 如果关羽向秦琼叫阵，则秦琼应声出战。命题符号化为：P：关羽向秦琼叫阵，Q：秦琼应声出战。P→Q成立。
◇ 李逵对戴宗说："我去酒肆一定帮你带壶酒回来"。命题符号化为：P=李逵去酒肆，Q=带壶酒回来，P→Q 成立。
（5）等价
给定两个命题P和Q，其复合命题P
Q，称作等价命题；当P和Q的真值相同时，PQ的真值为True，否则PQ的真值为False。
自然语言：“等价”、“当且仅当”、“充分必要”
例如，P：两个三角形全等；Q：两个三角形的三条对应边相等。PQ：两个三角形全等，当且仅当它们的三条对应边分别相等。
