关系代数是一种抽象的查询语言,用对关系的运算来表达查询,作为研究关系数据语言的数学工具。关系代数的运算对象是关系,运算结果亦为关系。关系代数用到的运算符包括四类:集合运算符、专门的关系运算符、算术比较符和逻辑运算符比较运算符和逻辑运算符是用来辅助专门的关系运算符进行操作的,所以按照运算符的不同,主要将关系代数分为传统的集合运算和专门的关系运算两类。

传统的集合运算是二目运算,包括并、交、差、广义笛卡尔积四种运算。
(1)并(Union)
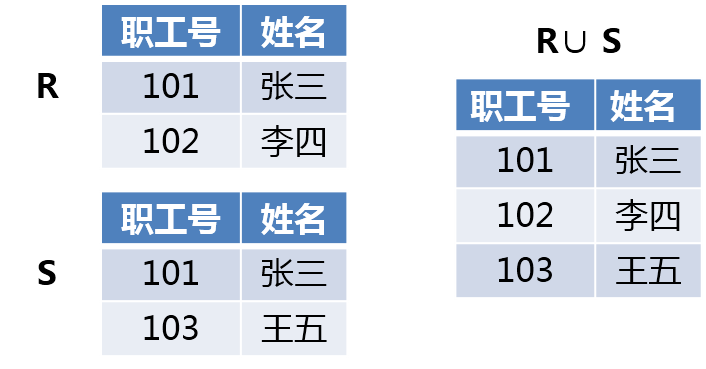
设关系R和关系S具有相同的目n(即两个关系都有n个属性),且相应的属性取自同一个域,则关系R与关系S的并由属于R且属于S的元组组成。其结果关系仍为n目关系。记作:R∪S={ t | t∈R ∨ t∈S }。
例如,有两个关系R和S,R∪S的结果如下图所示。
(2)交(Intersection Referential integrity)
设关系R和关系S具有相同的目n,且相应的属性取自同一个域,则关系R与关系S的交由既属于R又属于S的元组组成。其结果关系仍为n目关系。记作:R ∩ S = {t|t∈R∧t∈S}


(3)差(Difference)
设关系R和关系S具有相同的目n,且相应的属性取自同一个域,则关系R与关系S的差由属于R而不属于S的所有元组组成。其结果关系仍为n目关系。记作:R-S = { t | t∈R ∧ t∉S }
例如,有两个关系R和S,R-S的结果如下图所示。

(4)广义笛卡尔积(Extended cartesian product)
两个分别为n目和m目的关系R和S的广义笛卡尔积是一个(n+m)列的元组的集合。元组的前n列是关系R的一个元组,后m列是关系S的一个元组。若R有k1个元组,S有k2个元组,则关系R和关系S的广义笛卡尔积有k1×k2个元组。记作:R×S = { (t_r t_s ) | t_r ∈ R ∧ t_s∈S }
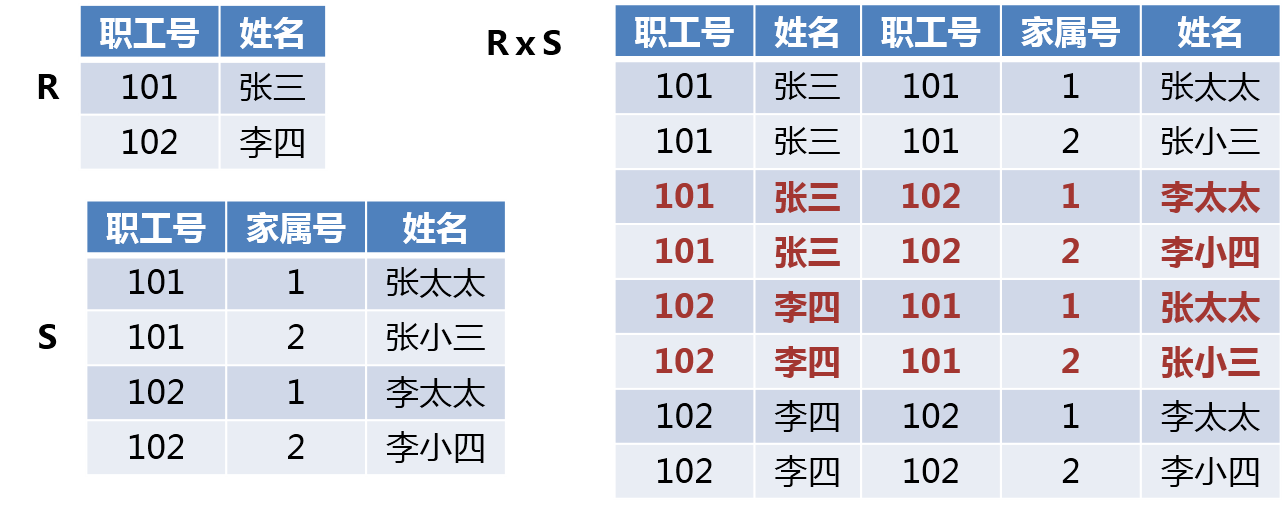
注意:广义的笛卡尔积穷尽了所有连接可能,这产生出很多无效的数据,比如上图中红色的都是无效的,张三和李四的家属李太太相连,毫无意义。很显然,职工号(第一列)和职工号(第三列)相等的连接方有意义。

专门的关系运算(Specific relation operations)包括选择、投影、连接、除等。
(1)选择(Selection)
选择又称为限制(Restriction)。它是在关系R中选择满足给定条件的诸元组,记作:σF(R) = { t | t∈R ∧ F(t) = '真' }。其中,F表示选择条件,它是一个逻辑表达式,取逻辑值‘真’或‘假’。

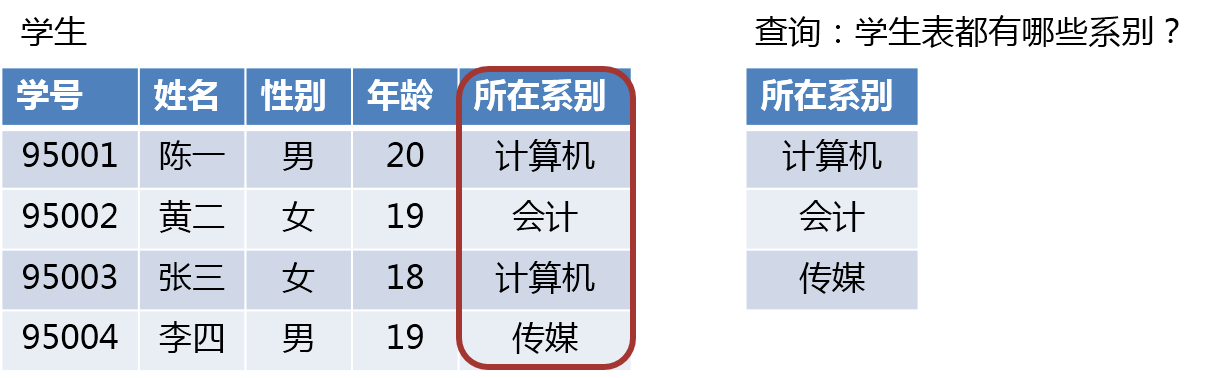
(2)投影(Projection)
关系R上的投影是从R中选择出若干属性列组成新的关系。记作:ΠA(R) = { t[A] | t∈R }。其中A为R中的属性列。

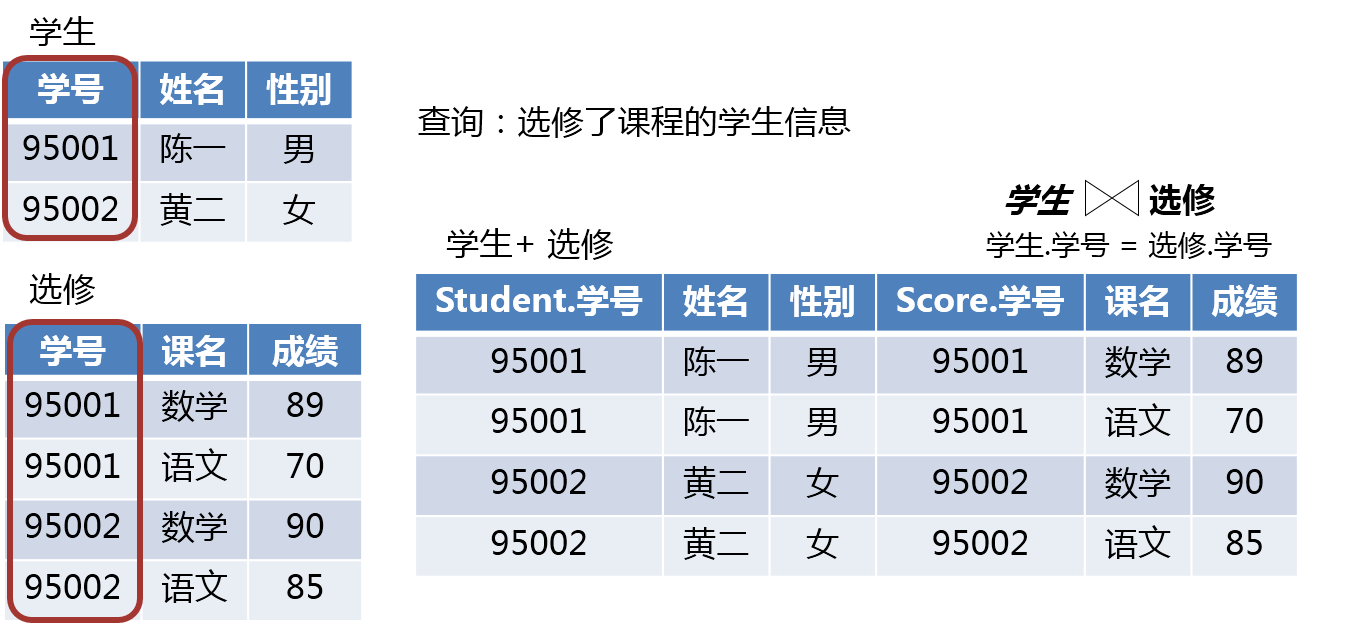
(3)连接(Join)
连接包括θ连接,自然连接,外连接,半连接。它是从两个关系的笛卡尔积中选取属性间满足一定条件的元组。
连接运算从R和S的笛卡尔积R×S中选取(R关系)在A属性组上的值与(S关系)在B属性组上值满足比较关系θ的元组。连接运算中有两种最为重要也最为常用的连接,一种是等值连接(equi-join),另一种是自然连接(Natural join)。
◇ θ为“=”的连接运算称为等值连接。它是从关系R与S的笛卡尔积中选取A、B属性值相等的那些元组。
◇ 自然连接(Natural join)是一种特殊的等值连接,它要求两个关系中进行比较的分量必须是相同的属性组,并且要在结果中把重复的属性去掉。
一般的连接操作是从行的角度进行运算。但自然连接还需要取消了重复列。