-
1 知识点回顾
-
2 练习与解析
-
3 章节自测
-
4 本章思考题

传说中米诺斯的宫殿里有一个半人半牛的怪物守着这个宫殿,每年雅典人都要为它献上七对少男少女作为供品。青年—希撒斯(Theseus)下决心要为人们除掉这一害,他与父亲爱琴约定:走时把小船上挂上黑帆,回来时,如果胜利了就换上白帆,如果还是黑帆,就说明儿子已经死了。 希撒斯成功的制服了怪物,但陷入迷宫里走不出来,而米诺斯王朝的公主爱上了他,帮他出逃。谁料在回去的途中,公主突然病亡,希撒斯悲痛于绝。悲伤中忘记了把黑帆换成白帆。 父亲海崖上眺望远方,一见黑帆,只道是儿子死了,绝望中跳海自尽。 从此,人们为了纪念他,就以他的名字给这个海命名——爱琴海。
在这个传说中,白帆表示胜利,黑帆表示死亡。也就是说有两个状态,一个状态是白帆,代表胜利,另一个状态是黑帆,代表死亡。

在计算机中,一位二进制数表示两个不同的信息,如:用0表示死亡、1表示胜利,更多位的二进制表示更复杂的信息,它的基数为2,进位规则是"逢二进一",借位规则是"借一当二"。
计算机为啥要用二进制?
(1)可行性:若使用十进制数,则需要这样的电子器件,它必须有能表示0—9数码的10个物理状态,这在技术上是相当困难的(目前为止没有完全解决),而使用二进制数,只需0,1两个状态,技术上易于实现,如开关的通与断,晶体管的导通与截止、磁介质的带磁与不带磁等。
(2)可靠性:二进制只有两种状态,数字传输处理不易出错。因为每位数据只有高低两个状态,当受到一定程度的干扰时,仍能可靠地分辨出它是高还是低。
(3)简易性:二进制运算法则比较简单。求和法则(3个) :0+0=0 , 0+1=1+0=1, 1+1=10
求积法则(3个):0×0=0,0×1=1×0=0,1×1=1,这就使计算机运算器的结构大大简化,控制也简单,较容易实现。
(4)逻辑性:二进制数0和1正好与逻辑量“真”和“假”相对应,因此用二进制数表示二值逻辑显得十分自然。

(1)存储单位与换算
0和1是计算机储存的基本单位,称为位,即一个0或1就是1位,8位(bit)为一个字节,在此基础上,换算率为2^10,即1024。
1B = 8bit (B:字节)
1KB = 1024B (KB:千字节)
1MB = 1024KB (MB:兆字节)
1GB = 1024MB (GB:吉字节)
1TB = 1024GB (TB:太字节)
1PB = 1024TB (PB:拍字节)
1EB = 1024PB (EB:艾字节)
ZB、YB、BB、NB、DB、……
(2)二进制的运算:
算术运算:
加:0+0=0,1+0=0+1=1,1+1=10
减:0-0=0,1-0=1,1-1=0,0-1=1
乘:0*0=0,0*1=1*0=0,1*1=1
除:0/1=0,1/1=1
逻辑运算:
与:0∧0=0,0∧1=0,1∧0=0,1∧1=1
或:0∨0=0,0∨1=1,1∨0=1,1∨1=1
非:not 0 = 1,not 1 = 0
(1)二进制转换为十进制,口诀:按权展开
课件源自于北京交通大学
(2)十进制转换为二进制,口诀:整数取余,小数分离
课件源自于北京交通大学
(3)二进制转换为八进制,口诀:三位一组整合
课件源自于北京交通大学,注意下图动画中,小数部分错误,应该是2,而不是1。
(4)八进制转换为二进制,口诀:一位拆分三位
课件源自于北京交通大学

数表示法依据不同的角度可以分为不同的类型。从数的是否带符号,可分为带符号数和无符号数;从数的符号的表示方法,可分为真值和机器数;从数制角度,可分为二进制数、十进制数、八进制数和十六进制数等;从计算机编码角度,数的表示法有原码、反码和补码;对于小数点的表示,可以分为定点表示法和浮点表示法。
(1)有符号数和无符号数
用一位二进制位表示数的符号:0表示正数,1表示负数,这种表示数的方法,称为有符号数的表示方法。所表示的数,叫做有符号的数。有符号的数其最高位为符号位。
如果将全部有效位都用来表示数的大小,这种数的表示方法,叫无符号数的表示方法,所表示的数,叫无符号数。
(2)定点数和浮点数
定点数:也称为整数,小数点固定在数的最右边。例如十进制整数-65的计算机内表示可以是11000001。
浮点数:也称为实数。小数点的位置是浮动的,其范围和精度分别用阶码和尾数来表示。在计算机中,为了提高数据表示精度,必须唯一地表示小数点的位置,因此规定浮点数必须写成规范化的形式,即数值部分是一个小数,小数点前的数字是零,小数点后的第一位数字不是零。如:-6.375 D = -110.011(B) = -0.110011×2^+11

(3)真值与机器数
真值就是利用"+"、"-"表示数的符号,数值部分为数的绝对值。例如:N1=+1101001B= +105;N2=-1101001B=-105。数的真值可以使用二进制形式、八进制形式、十进制形式或十六进制形式表示。
机器数就是在机器中用最高位表示数的符号,其它位表示数值的大小。这时最高位叫做符号位,规定用“0"表示正,“1’’表示负。这样对于n位二进制数,如果它是一个带符号的数,则最高位Bn-1就表示数的符号,剩下的n-1位表示数的大小。简单的说,机器数就是数据在机器中的二进制表示形式,机器数所表示的值称为该机器数的“真值”。
例如:一个带符号的数11101001B,最高位"1"为符号位,代表“-”其它位为数的值,它的真值为:-1101001B(-105)。
(3)机器数表示法
原码:是一种直观的机器数表示法,用最高位表示符号,符号位为0表示该数为正,符号位为1表示该数为负,数值部分为原数的绝对值。如:-5的原码为10000101,+9的原码为00001001。
反码:正数的反码与原码相同,负数的反码是对其原码除符号位外的部分求反。符号位也参与计算。如:-5的反码为11111010,+9的反码为00001001。
补码:正数的补码和原码相同,负数的补码是在其反码的最后一位上加1。如:-5的补码为11111011,+9的补码为00001001。

如果用原码计算,则出现两个问题,一是0不唯一,+0用00000000表示,-0用10000000表示,二是计算不正确,-5+9=10000101+00001001=10001110 = -14 D
如果用反码计算,同样出现两个问题,一是0不唯一,+0用00000000表示,-0用11111111表示,二是计算也不正确,-5+9=11111010+00001001=1 00000011,最高位溢出舍去,即-5+9=00000011=+3 D
如果用补码计算,0的表示唯一,+0用00000000表示,-0用1 00000000表示,最高位溢出,舍去,即00000000,其次,计算正确。-5+9=11111011+00001001=1 00000100,最高位溢出,舍去,即+4D。
结论:计算机中关于数的表示采用二进制补码进行存储和计算。
以下课件源自于北京交通大学,课件中反码和补码的中文字有误。
在使用计算机进行数据处理时,字符型数据是非常普遍的,字符型数据包括西文字符和中文字符。
(1)西文字符
西文字符包括字母、数字与符号等。它们在计算机中用二进制进行统一编码。ASCII码即美国标准信息交换码,已被国际标准化组织定为国际标准。
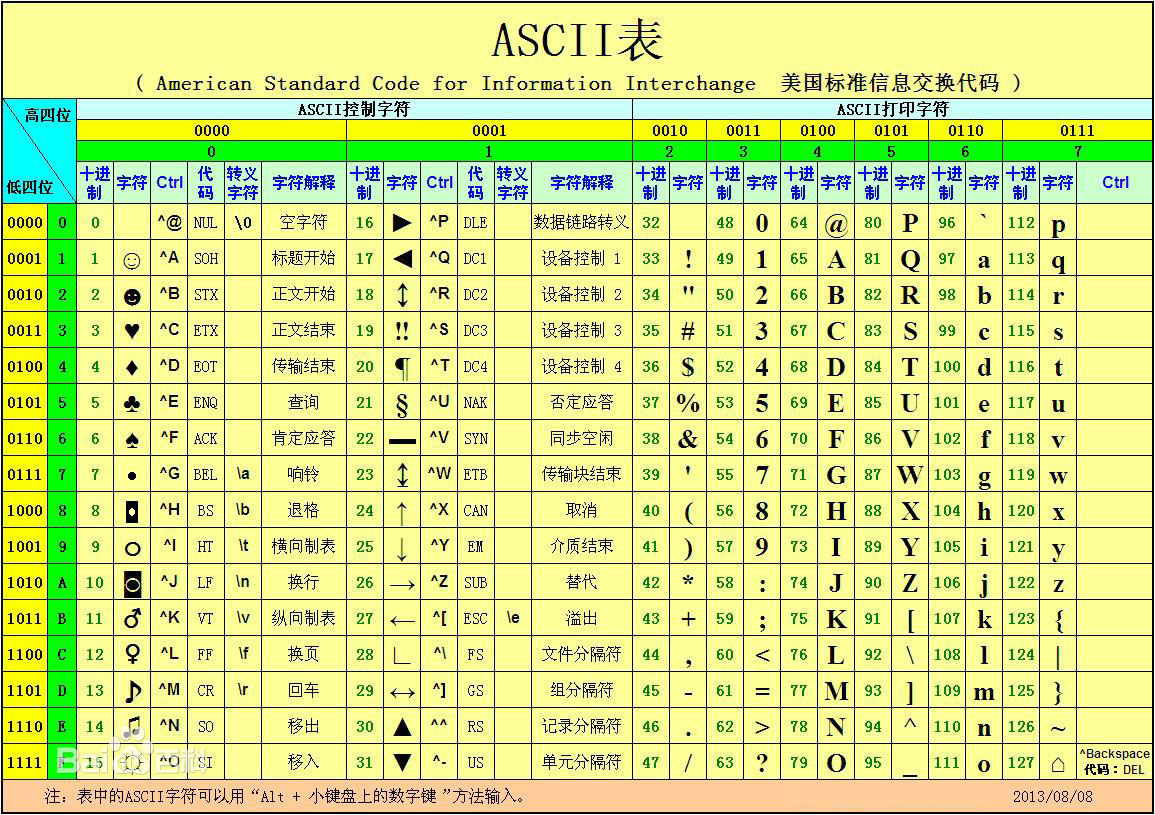
(2)中文字符。
汉字进入计算机比较困难,主要是因为汉字数量庞大、字形复杂、存在大量一音多字和一字多音的现象。所以,根据应用目的的不同,将汉字编码分为外码、交换码、机内码和字形码四种。
外码也叫输入码,是用来将汉字输入到计算机中的一组键盘符号。常用的输入码有拼音码、五笔字型码、自然码、表形码、认知码、区位码和电报码等,一种好的编码应有编码规则简单、易学好记、操作方便、重码率低、输入速度快等优点。如“保”字,用全拼,输入码为码为“BAO”,用区位码,输入码为“1703 ”,用五笔字型则为“WKS”。
计算机只识别由0、1组成的代码,所以需要将输入码进行信息交换,1981年制定了中华人民共和国国家标准GB2312--80《信息交换用汉字编码字符集--基本集》,即国标码,国标码=区位码+2020H。
国标码是汉字信息交换的标准编码,但因其前后字节的最高位为0,与ASCII码发生冲突,如“保”字,国标码为31H和23H,而西文字符“1”和“#”的ASCII也为31H和23H,现假如内存中有两个字节为31H和23H,这到底是一个汉字?,还是两个西文字符“1”和“#”于是就出现了二义性。
显然,国标码是不可能在计算机内部直接采用的,于是,汉字的机内码采用变形的国标码,其变换方法为:将国标码的每个字节都加上128,即将两个字节的最高位由0改1,其余7位不变。如:由上面我们知道,“保”字的国标码为3123H,前字节为00110001B,后字节为00100011B,高位改1为10110001B和10100011B 即为B1A3H,因此,汉字的机内码就是B1A3H。即机内码=国标码+8080H。
汉字字形码是汉字字库中存储的汉字字形的数字化信息,用于汉字的现实和打印。通常有两种表示方式:点阵和矢量表示方法。

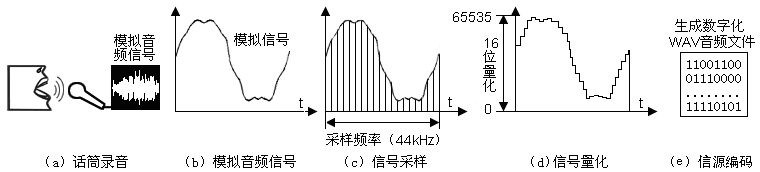
声音、图形、视频等信息,需要转换成二进制数后计算机才能存储和处理。将模拟信号转换成二进制数的过程称为数字化处理。音频的数字化处理需要经过话筒录音、模拟音频信号、信号采样、信号量化、信源编码。其中,
采样:在固定时间间隔内,对模拟音频信号截取振幅值。单位时间内采样次数(采样频率)越多,数字信号就越接近原声。
量化:将信号连续取值为有限多个离散值。
编码:将采集的原始数据,按文件类型(如WAV、MP3等)编码,再加上音频文件的头部,就得到了一个数字音频文件。
数码相机、扫描仪等设备可以直接对自然图像进行数字化处理,然后通过设备与计算机的接口传输到计算机内部,并用0和1,对图像进行存储,图像输出到显示器、打印机或电视机时,必须将离散化的数字图像合成一副图形处理设备能够接受的自然图像。
点阵图像有二值图像、灰度图像、和彩色图像。矢量图像文件较小;图像放大或缩小不影响图像的分辨率。难以表示色彩丰富的逼真效果;无统一标准格式;廉价设备无法点阵图形输到计算机并矢量化。








