题目一:珍贵的宝石(分治法)
珍贵的宝石,晶莹剔透,不小心混入到了高仿玻璃制品中,真正的宝石比玻璃制品重,除此之外,无法肉眼区分它们。现给你一架托盘天平,聪明的你设计一个算法,如何才能快速将宝石从高仿玻璃制品重找出来?
输入一个整数n,代表有n-1个高仿玻璃制品和那个要找的宝石,输出天平称重的次数。请根据下面的伪代码,绘制Raptor流程图,计算出结果。
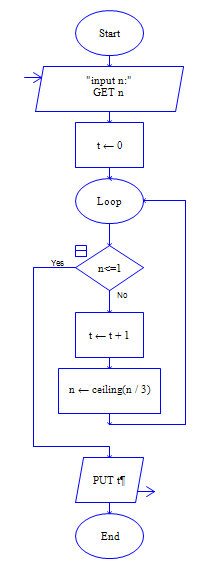
input n, t=0
while n>1 do
t=t+1
n=(n+2)/3
endwhile
output t
-----------------------------------------------------------------------------------------------
题目二:顺序查找(查找技术)
给定n个整数,请你在这n个整数中查找是否包含指定的数值,如果包含,输出该数的位置,如果没找到,则输出未找到指定数值。
输入:首先输入n,代表n个整数,随后输入n个整数,最后,输入一个数,表示待查找的数。
输出:该数的位置
样例输入1:
6
8 6 9 3 2 7
5
样例输出1:
not find 5
样例输入2:
7
8 6 9 3 2 7 9
9
样例输出2:
3
请根据下面的伪代码,绘制Raptor流程图。
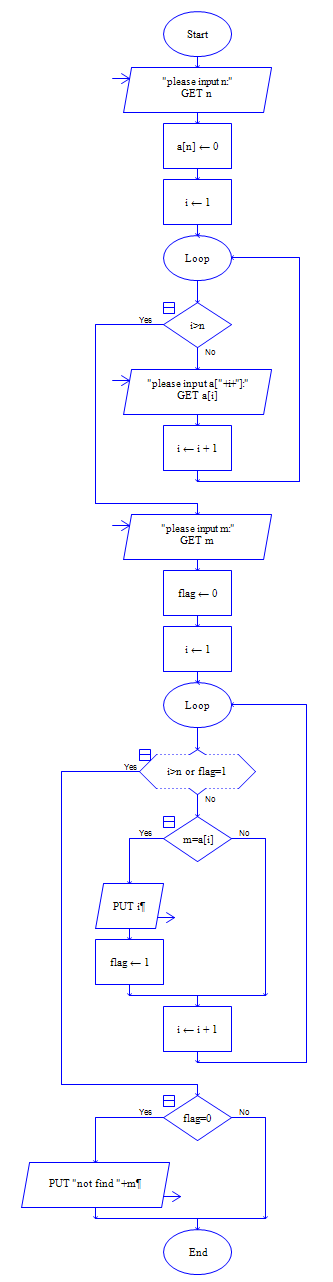
input n
for i=1 to n
input a[i]
endfor
input m
flag=0
i=1
while flag=0 and i<=n do
if a[i]=m then
output i
flag=1
endif
i=i+1
endwhile
if flag=0 then
output "not find."
endif
-----------------------------------------------------------------------------------------------
题目三:简单排序(排序技术)
给定n个整数,请你对这些整数进行升序排列并输出。下面的伪代码的功能是比较排序,请根据下面的伪代码,绘制Raptor流程图。
输入:首先输入n,代表有n个整数,随后输入这n个整数
输出:排序后的n个整数
样例输入:
6
8 6 9 3 2 7
样例输出:
2 3 6 7 8 9
伪代码如下:
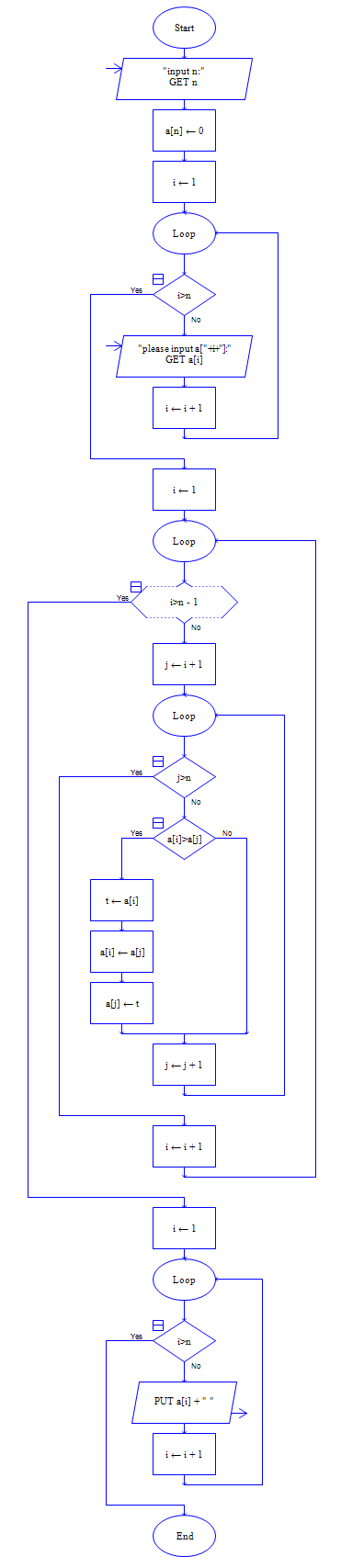
input n
a[n]=0
for i=1 to n
input a[i]
endfor
for i =1 to n-1
for j=i+1 to n
if a[i]>a[j] then
t=a[i]
a[i]=a[j]
a[j]=t
endif
endfor
enfor
------------------------------------------------------------------------------------------------
题目四:合法抢劫(贪心算法)
超市举行活动,给你一个箱子。超市里面的东西只要能装进这个箱子就可以免费拿走。如果物品都是可以分割的(如:大米、金粉),那么最优策略是什么?
输入:首先输入两个正整数s,m。s表示有s个物品。接下来输入s个物品的v,w。v表示单位重量的价值,w表示重量。
输出:背包内的物品的价值和。
样例输入:
3 15
5 10
2 8
3 9
样例输出:65
分析:背包荷载15kg,现有3个物品,单位重量的价值分别为5,、2、3,重量分别为10、8、9。贪心策略是什么?拿最贵的?扛一个冰箱走,那是笨蛋,拿性价比最高的?如果商品可分,回答:Yes。拿金条、金砖、金戒子、如果拿不了整个的,还可以切割为小块,或磨成粉,带走。
3个物品,谁的性价比最高?物品1:单位价值为5、物品2:单位价值为2,物品3:单位价值为3。排序后,显然是物品1、物品3、物品2,也就是说,先可物品1装,可以装重量10,总价值为50,背包荷载重量还剩5,由于没有物品1了,只能拿性价比第二大的物品3了,物品3重量还有9,不过背包只剩下5了,不能全拿,由于物品可分,那就拿重量5的物品,3,总价值为15,共计拿了总价值65的物品1和物品3。
请根据下面的伪代码,绘制Raptor流程图,计算出结果。
伪代码如下:
input n,w // 输入物品数量和背包重量
for i =1 to n // 输入每个物品的单位价值和重量
input a[i]
input b[i]
endfor
for i=1 to n-1 // 排序
for j=i+1 to n
if a[i]<a[j] then
t=a[i], a[i]=a[j], a[j]=t
t=b[i], b[i]=b[j], b[j]=t
endif
endfor
endfor
i=1
sum=0
while w>0 do
if w>=b[i] then
sum=sum+b[i]*a[i]
w=w-b[i]
else
sum=sum+w*a[i]
w=0
endif
i=i+1
endwhile
output sum

-------------------------------------------------------------------------------------------------
题目五:渊子赛马(贪心算法)
赛马是一古老的游戏,早在公元前四世纪的中国,处在诸侯割据的状态,历史上称为“战国时期”。在魏国作官的孙膑,因为受到同僚庞涓的迫害,被齐国使臣救出后,到达齐国国都。赛马是当时最受齐国贵族欢迎的娱乐项目。上至国王,下到大臣,常常以赛马取乐,并以重金赌输赢。田忌多次与国王及其他大臣赌输赢,屡赌屡输。一天他赛马又输了,回家后闷闷不乐。孙膑安慰他说:“下次有机会带我到马场看看,也许我能帮你。”孙膑仔细观察后发现,田忌的马和其他人的马相差并不远,只是策略运用不当,以致失败。比赛前田忌按照孙膑的主意,用上等马鞍将下等马装饰起来,冒充上等马,与齐王的上等马比赛。第二场比赛,还是按照孙膑的安排,田忌用自己的上等马与国王的中等马比赛,在一片喝彩中,只见田忌的马竟然冲到齐王的马前面,赢了第二场。关键的第三场,田忌的中等马和国王的下等马比赛,田忌的马又一次冲到国王的马前面,结果二比一,田忌赢了国王。
就是这么简单,现在渊子也来赛一赛马。假设每匹马都有恒定的速度,所以速度大的马一定比速度小的马先到终点(没有意外!!)。不允许出现平局。最后谁赢的场数多于一半(不包括一半),谁就是赢家(可能没有赢家)。渊子有n匹马参加比赛。对手的马的数量与渊子马的数量一样,并且知道所有的马的速度。聪明的你来预测一下这场世纪之战的结果,看看渊子能否赢得比赛。
输入:先输入n,代表每队匹马数量,然后分别输入渊子的n匹马速度和对手的n匹马速度。
输出:在你的安排下,如果渊子能赢得比赛就输出Yes,否则输出No
样例输入1:
5
3 3 2 4 5
1 2 3 4 5
样例输出1:Yes
样例输入2:
4
2 2 1 2
2 2 3 1
样例输出2:No
分析:渊子赛马的贪心策略是什么?
如果渊子当前的马匹速度比对手当前的马匹速度慢,那么就pk掉对手的最快的马,让当前马死得其所,反正是死,索性死得价值最大。如同下军旗,师长后面是炸弹,死得其所。
伪代码如下:
主调函数:
input n
a[n]=0
b[n]=0
for i=1 to n // 输入渊子的马匹速度
input a[i]
endfor
for i=1 to n // 输入对手的马匹速度
input b[i]
endfor
sort(a,n) // 渊子的马匹速度进行排序
sort(b,n) // 对手的马匹速度进行排序
i=1
j=1
flag=0
while i<=n and flag=0 do
if a[i]<=b[j] then
lose=lose+1
else
win=win+1
j=j+1
endif
if win>n/2 or lose>n/2 then
flag=1
endif
i=i+1
endwhile
if win>lose then
output "Yes"
else
output "No"
endif
被调函数:
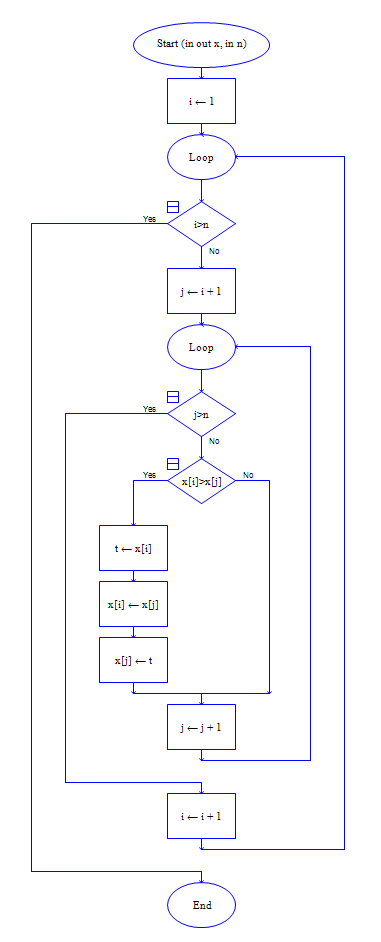
function sort ( x,n ) // 排序函数
for i =1 to n-1
for j=i+1 to n
if x[i]>x[j] then
t=x[i]
x[i]=x[j]
x[j]=t
endif
endfor
endfor
endfunction
主调函数:
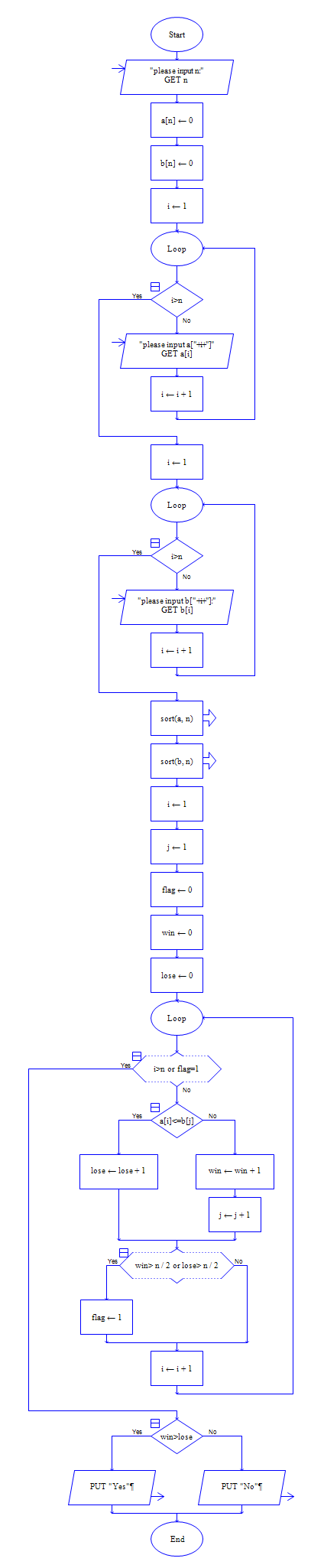
被调函数: