1.  能举例说明动态规划算法思想

2.  能使用动态规划设计算法，进行问题求解

3.  能使用动态规划分析问题，绘制Raptor流程图、编写Python代码

1、多阶段决策——集体的力量

2、多阶段决策——杜绝不劳而获

多阶段决策过程，是指这样一类的决策问题：由问题的特性，可将过程按时间、空间等标志分为若干个互相联系又相互区别的阶段，在它的每一个阶段都需要做出决策，从而使整个过程达到最好的效果。

（1）什么是动态规划？

20世纪50年代，美国数学家Bellman在研究多阶段决策过程的优化问题时，提出了著名的最优化原理。这种优化理论，把多阶段过程转化为一系列单阶段问题，利用各阶段之间的关系，逐个求解，从而创立了解决这类过程优化问题的新方法——动态规划。

（2）动态规划的特点

◇ 决策者需要作出时间上有先后之别的多次决策。

◇ 前一次决策的选择将直接影响到后一次决策，后一次决策的状态取决于前一次决策的结果。

◇ 决策者关心的是多次决策的最终结果，而不是各决策的即时结果。

（3）基本概念

◇阶段：把一个复杂的决策问题按时间或空间特征分解为若干个相互联系的阶段，以便顺序求解。一般用 k 表示。阶段是对整个过程的自然划分。

◇状态：每个阶段有若干个状态，表示某一个阶段决策面临的条件或所处的位置。一般用 s 表示。

◇决策：就是关于状态的选择，是决策者从给定阶段状态触发对下一阶段状态作出的选择。一般用Xk=XK(SK)表示。表示k阶段，状态Sk时的决策。

◇状态转移方程：一个状态到另一个状态的转移过程由状态转移过程描述。大多数情况下可以用数学公式表达。

◇ 指标函数：分为阶段函数和过程函数（目标函数）两种。它是全过程或子过程或各阶段上确定数量的函数。如费用、成本、距离、利润、时间等。

◇ 最优解：对指标函数求解，称为最优解。

（4）动态规划步骤

划分阶段à选择状态à确定决策à写出状态转移方程à确定决策变量取值范围（包括边界条件）à写出指标函数递推公式à逆序求解。

（5）适用条件

◇最优化子结构

最优化原理可这样阐述：一个最优化策略具有这样的性质，不论过去状态和决策如何，

对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简言之，一个最优化

策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。

◇无后效性

将各阶段按照一定的次序排列好之后，对于某个给定的阶段状态，它以前各阶段的状态

无法直接影响它未来的决策，而只能通过当前的这个状态。换句话说，每个状态都是过去历

史的一个完整总结。这就是无后效性。

◇重叠子问题

子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。

（6）动态规划的优缺点

优点：解决复杂问题、找到全局最优解、可以得到一组解。

缺点：依赖于经验和技巧、无后效性局限大、维数灾难。

（7）动态规划算法框架

input 阶段变量，状态变量，决策变量，状态数组

for i = 阶段最大值 downto 1 step -1        // 倒推每一个阶段

   for j = 状态最小值 to 状态最大值          // 枚举阶段i的每一个状态

       for k = 决策最小值 to 决策最大值     // 枚举 i 阶段 j 状态下的每一种决策

            目标函数

output 最优方案

示例：最短路径问题

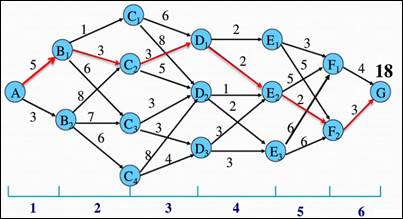
解析：

（1）阶段变量：按空间划分阶段。分为6个阶段。K=1, … , 6

（2）状态变量：可用城市编号作为状态变量。S1={A}，S2={B1,B2}，S3={C1,C2,C3,C4}，S4={D1,D2,D3}，S5={E1,E2,E3}，S6={F1,F2}，S7={G}。

（3）决策变量：也可用城市编号作为决策变量。X1(S1)=A，X2(S2)=B1，X3(S3)=C2，X4(S4)=D1，X5(S5)=E2，X6(S6)=F2，X7(S7)=G

（4）写出状态转移方程：Sk+1=Xk

（5）指标函数

阶段函数：V_k=( S_k，X_K )

目标函数：f_k（S_k）=min{V_k+f_k+1（S_k+1）}

（6）逆序求解：从k=6开始计算。

K=6

    f₆(F₁)=4，f₆(F₂)=3

K=5

    f₅(E₁)=min{3+f₆(F₁)=7*，5+f₆(F₂)=8}=7

    f₅(E₂)=min{5+f₆(F₁)=9，2+f₆(F₂)=5*}=5

    f₅(E₃)=min{6+f₆(F₁)=10，6+f₆(F₂)=9*}=9

K=4

    f₄(D₁)=min{2+f₅(E₁)=9，2+f₅(E₂)=7*}=7

    f₄(D₂)=min{1+f₅(E₂)=6*，2+f₅(E₃)=11}=6

    f₄(D₃)=min{3+f₅(E₂)=8*，3+f₅(E₃)=12}=8

K=3

    f₃(C₁)=min{6+f₄(D₁)=13*，8+f₄(D₂)=14}=13

    f₃(C₂)=min{3+f₄(D₁)=10*，5+f₄(D₂)=11}=10

    f₃(C₃)=min{3+f₄(D₂)=9*，3+f₄(D₃)=11}=9

f₃(C₄)=min{8+f₄(D₂)=14，4+f₄(D₃)=12*}=12

K=2

    f₂(B₁)=min{1+f₃(C₁)=14，3+f₃(C₂)=13*，

               6+f₃(C₃)=15}=13

    f₂(B₂)=min{8+f3(C₂)=18，7+f₃(C₃)=16*，

               6+f₃(C₄)=18}=16

K=1

    f₁(A)=min{5+f₂(B₁)=18*，3+f₂(B₂)=19}=18

故，最短路径为：A à B₁ à C₂ à D₁ à E₂ à F₂ à G。