1、分而治之,各个击破。
2、分治法——分布式设计的基础,勿以善小而不为,勿以恶小而为之。


分治法,分割问题、各个击破。将一个大问题,分割成许多小问题。如果小问题还是很难,就继续分割成更小的问题,直到问题变得容易解决。分割出来的小问题,称作「子问题」。解决一个问题,等价于解决所有子问题。用树形图表达原问题与子问题的关系,最好不过!
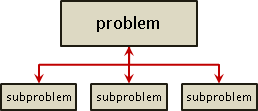
分治法着重分割问题的方式── 要怎么分割问题,使得子问题简单又好算?
示例:分解动作
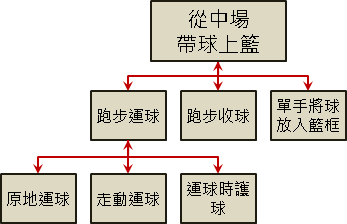
想要学习「从中场带球上篮」,我们可以将此动作分割为「跑步运球」、「跑步收球」、「单手将球放入篮框」等动作,分别学习。每一项动作都熟练之后,组合起来便是带球上篮了。如果觉得「跑步运球」还是太难,可以更细分成「原地运球」、「走动运球」、「运球时护球」等动作,克服了之后便能够顺利解决「跑步运球」的问题了。
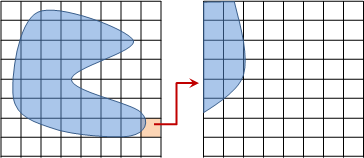
示例:方格求面积
左边为原问题,右边放大并细分的图是其中一个子问题。

示例1:二分求幂
计算机模拟手工计算 2^159 = ?
解析:
手工计算2^159,怎么计算?自然是判断指数,如果指数为奇数,则,2^奇数幂 = 2* 2^奇数幂-1,如:2^159= 2 * 2^158,否则,指数为偶数幂,2^偶数幂 =4^偶数幂的一半。如:2^158 =(2^2)^79 = 4^79。
求解过程,
2^159 =?
=2*2^158
=2*4^79
=2*4*4^78
=2*(4*16^39)
=……
=2*(4*(16*256*(256^2)* (256^2^2^2)^2))
伪代码如下:
被调函数
function f(x,n) // 求 x^n
if n=1 then
return x
endif
if n mod 2=1 then
return x*f(x, n-1)
else
return f(x^2, n/2)
endif
endfunction
流程图如下:
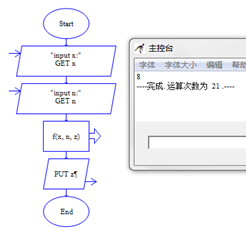
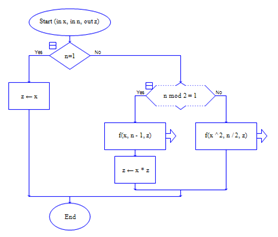
示例2:找假币
16个硬币中,混进了1枚假币。现在知道假币的重量比真币的质量要轻。给你一个天平,请用最快的时间把那个可恶的假币找出来。
解析:
当硬币总数为一,那么该币就是假币。当硬币总数为二,则两枚硬币分别放在天平两端秤重,较轻的一端就是假币。当硬币总数为三以上,一定有办法找出假币,以下介绍两种策略。采用递增法。每次取两枚硬币,放在天平两端秤重。当天平平衡,表示这两枚硬币都是真币,接着继续处理剩余硬币。当天平倾斜,比较轻的硬币就是假币。

采用分治法。两枚硬币放在天平两端秤重,当天平平衡,表示这两枚硬币都是真币。接着只剩下 N-2 枚硬币要寻找假币 ── 问题递归缩小了!剩下 N-2 枚,太多了一点。一次取多一点硬币,同时放在天平两端秤,问题就能缩小更多了!把所有硬币平均分成三份,取两份放在天平两端秤重。当天平平衡,表示剩下的一份含有假币,问题一次便缩小为 1/3 。当天平倾斜,表示比较轻的一份含有假币,问题一次便缩小为 1/3 。

伪代码如下:
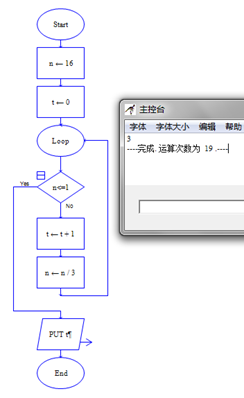
input n=16, t=0
while n>1 do
t=t+1
n=n/3
endwhile
output t
流程图如下: