题目一、水仙花数（枚举法）

春天是鲜花的季节，MM们也是花枝招展，水仙花就是其中最迷人的代表，数学上有个水仙花数，他是这样定义的：

“水仙花数”是指一个三位数，它的各位数字的立方和等于其本身，比如：153=1^3+5^3+3^3。请你用枚举法输出所有水仙花数。

----------------------------------------------------------------------------------------------------------------------------

分析：

（1）水仙花数是一个三位数，所以其范围应该为：【0,999】

（2）其各位的数字的立方和等于其本身，即：n=a^3+b^3+c^3

（3）需要在【0,999】范围内，逐一排查，搜索满足 n=a^3+b^3+c^3 式子的n。

故此，

（1）枚举范围：【0,999】；

（2）约束条件：n=a^3+b^3+c^3

想办法求出这个三位数的各位数字成为关键。解决方法如下：

百位上的数设为a，a=floor(n/100)，即：n/100后取整，raptor中的取整函数：floor（下取整）、ceiling（上取整）。

十位上的数设为b，b有两种求解方法：1）b=floor(n/10) mod 10；2）b=floor((n mod 100)/10)

个位上的数设为c，c=n mod 10

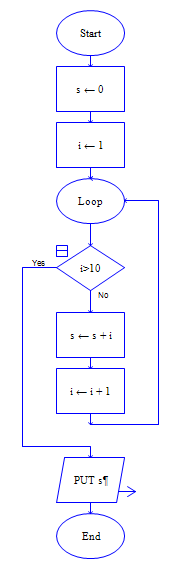
◇ 伪代码：

for i = 100 to 999

    a=floor(i/100)

    b=floor(i/10) mod 10

    c=i mod 10

    if i=a^3+b^3+c^3 then

         output i

    endif

endfor

◇ 流程图

----------------------------------------------------------------------------------------------------------------------------

题目二、韩信点兵（枚举法）

相传韩信才智过人，从不直接清点自己军队的人数，只要让士兵先后以三人一排、五人一排、七人一排地变换队形，而他每次只掠一眼队伍的排尾就知道总人数了。一次，韩信带1500名兵士打仗，战死四五百人，站3人一排，多出2人；站5人一排，多出4人；站7人一排，多出6人。韩信很快说出人数，现在请你用枚举法计算一下韩信剩余的士兵人数。

---------------------------------------------------------------------------------------------------------------------------------

分析：

（1）韩信带1500名士兵去打仗，战死四五百人，即：剩下一千多人。

（2）站3人一排，多出2人；站5人一排，多出4人；站7人一排，多出6人。即：剩余人数和3除，余2人；和5除，余4人；和7除余6人。

故此，

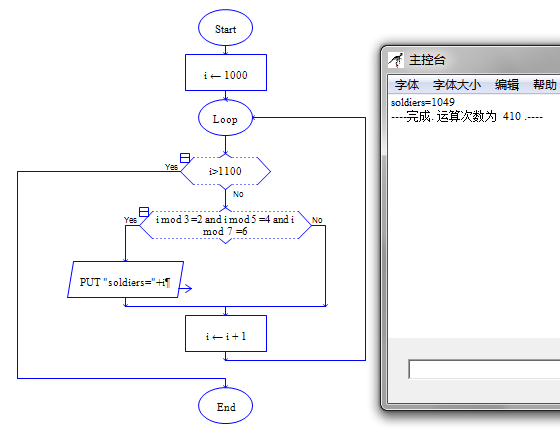
（1）枚举范围：【1000,1100】

（2）约束条件：n mod 3 =2 and n mod 5 =4 and n mod 7 =6

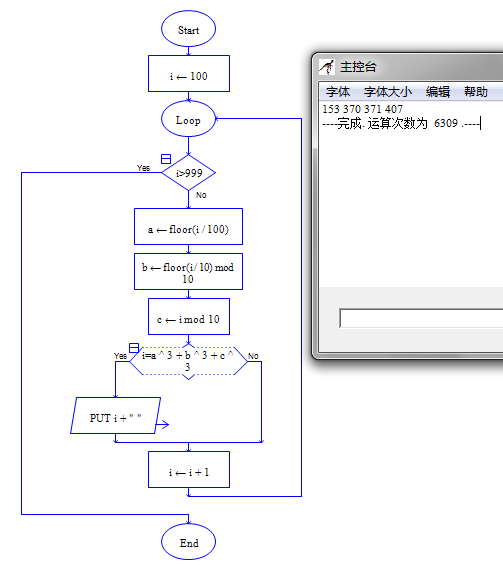
◇  伪代码：

for i=1000 to 1100

  if i mod 3 =2 and i mod 5 =4 and i mod 7 =6 then

       output "soldiers="+i

  endif

endfor

◇  流程图：

---------------------------------------------------------------------------------------------------------------------------------

题目三、棋迷俱乐部（枚举法、迭代法）

张三、李四、王五三个棋迷，定期去文化宫下棋。张三每五天来一次，李四每六天来一次，王五每九天来一次。问每过多少天他们才能一起在文化宫下棋？提示：可以用最小公倍数求解（迭代法）、也可以用枚举法求解。

---------------------------------------------------------------------------------------------------------------------------------

分析：

张三每五天来一次，李四每六天来一次，王五每九天来一次。即：求5、6、9的最小公倍数，即：90。

（1）迭代法求解

方法1：非递归实现：

m=5，n=6，p=9，辗转相除法求出m和n的最大公约数 1，然后，再求出m和n的最小公倍数 p=30。再次辗转相除法求p和q的最大公约数：3，再求出最小公倍数：r=90。

伪代码如下：

主调函数：

m=5

n=6

p=9

q=m*n/gcd(m,n)

r=p*q/gcd(p,q)

output r

被调函数：

function gcd ( x , y )

    r = x mod y

    while r !=0 do

          x = y

          y = r

          r = x mod y

    end while

    return y

end function

流程图如下：

        

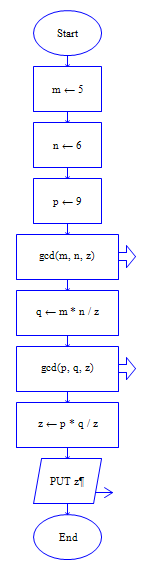
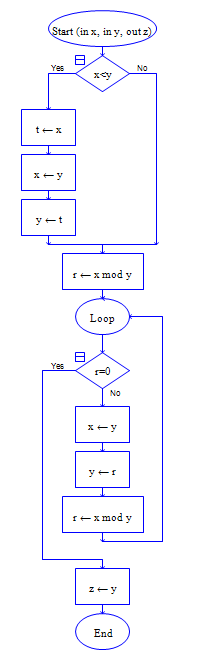
            主调函数                              被调函数

方法2：递归实现：

递归式：gcd（n，m mod n）

递归出口：n=1

界函数：gcd（n，m mod n）

伪代码如下：

主调函数代码不变，同上。

被调函数：

function gcd ( x , y )

    r = x mod y

    if r = 0 then

          return y

    else

          return gcd ( y , r)

    end if

end function

流程图：

主调函数流程图不变，同上。

被调函数流程图如下：

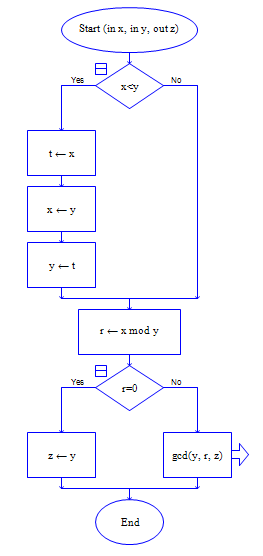
（2）枚举法求解

枚举范围：【1，？】

约束条件：days mod 5 =0 and days mod 6=0 and days mod 9=0

枚举没有结束范围，怎么办？可以用while语句实现，循环次数未知。

伪代码：

days =0

flag =1

while flag=1 do

    days = days +1

    if days mod 5 =0 and days mod 6=0 and days mod 9=0 then

        flag=0

    end if

endwhile

output days

流程图如下：

---------------------------------------------------------------------------------------------------------------------------------

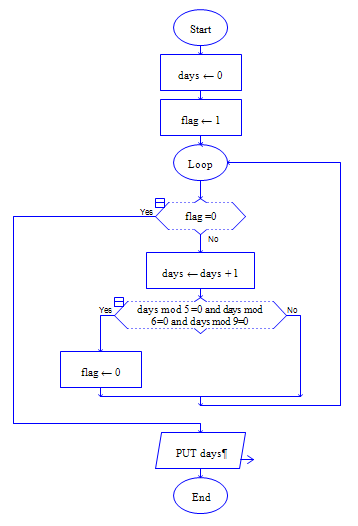
题目四、神秘三位数（递归法、枚举法）

有这样一个3位数，组成它的3个数字阶乘之和正好等于它的本身。即：abc=a!+b!+c!，请你用递归法搜索一下这样的3位数。

---------------------------------------------------------------------------------------------------------------------------------

分析：

和第一题类似，要先将这个数的个位、十位、百位分解出来，然后分别求阶乘，最后求和。

伪代码：

主调函数：

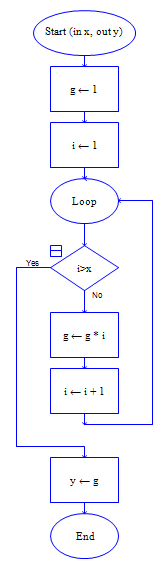
for i=100 to 999

    a=floor( i/100 )

    b=floor( i/10 ) mod 10

    c=i mod 10

    if i = fact(a) + fact(b) +fact(c)

          output i

    endif

被调函数：

function fact ( x )

    f=1

    for i =1 to x

          f =f *i

    endfor

    return f

endfunction

流程图：

      

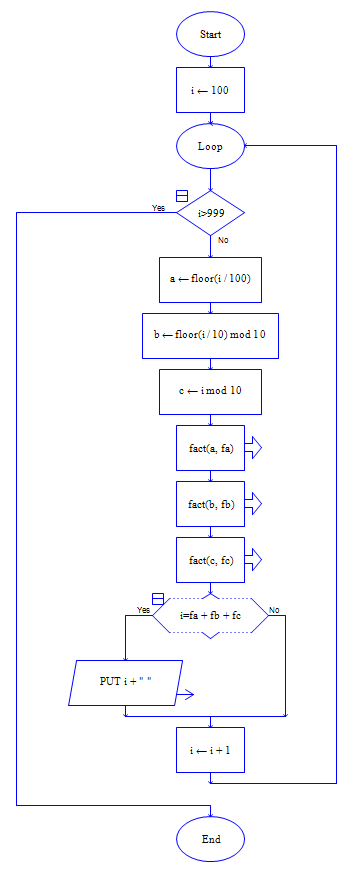
                                             主调函数                                               被调函数

递归实现：

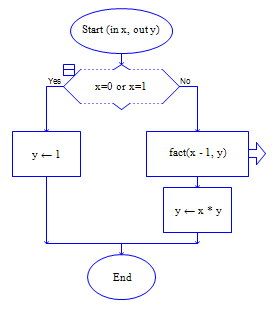
主调函数的伪代码和流程图都不变。被调函数的伪代码如下：

function fact ( x )

    if x=0 or x=1 then

         return 1

     else

          return x*fact ( x )

end function

流程图如下：

---------------------------------------------------------------------------------------------------------------------------------

题目五、经济大恐慌（递推法）

公元2505 年 1 月 1 日，发生了世界经济大恐荒。从那天起，物价飞涨。第一天一个馒头只要一元，第二天就要三元，第三天要卖六元，第四天要卖十元，以此类推。请你问第10天馒头卖多少钱？请你用递推法求解。

---------------------------------------------------------------------------------------------------------------------------------

分析：

第 1 天 —— 1 元

第 2 天 —— 3 元

第 3 天 —— 6 元

第 4 天 —— 10 元

......

第 10 天 —— ？ 元

本题为递推法，第 i 天的钱数 = i-1 天 的钱数 + i，可以用数组实现、也可以用通项公式实现。

方法1：递推法

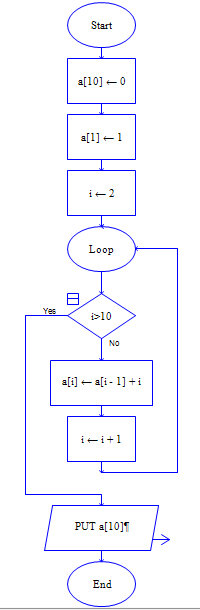
（1）伪代码如下：

a[10]={0}

a[1]=1

for i = 2 to 10

    a[i]=a[i-1]+i

endfor

（2）流程图如下：

方法2：通项公式法

        a1=1

        a2=a1+2

        a3=a2+3

        ......

+)    an=an-1+n

----------------------

        a10=1+2+3+...+n

              =（1/2）*n*（a1+an）

              =10*11/2

              =55

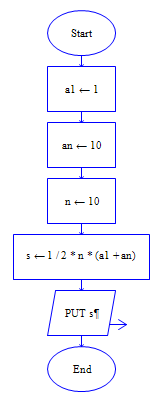
（1）伪代码1：

a1=1

an=10

n=10

s=(1/2)*n*(a1+an)

output s

（2）伪代码2：

s=0

for i =1 to 10

      s = s + i

endfor

output s