1、迭代法也称辗转法,是一种不断用变量的旧值递推新值的过程,结合时政谈谈"新工科"与产业升级。
2、习近平总书记在党的十九大报告中指出:中国特色社会主义进入了新时代,意味着近代以来久经磨难的中华民族迎来了从站起来、富起来到强起来的伟大飞跃,迎来了实现中华民族伟大复兴的光明前景。在迭代的过程中,凝聚着老一辈中国人的奋斗,鼓励学生在百年未有之大变局的时代,应该更加奋发努力学习。


迭代法也称辗转法,是一种不断用变量的旧值递推新值的过程,跟迭代法相对应的是直接法(或者称为一次解法),即一次性解决问题。迭代算法是用计算机解决问题的一种基本方法,它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值,迭代法又分为精确迭代和近似迭代。


示例1:最大公约数问题
请用辗转相除法求两自然数m,n的最大公约数是多少?如14和6的最大公约数为2。
解析:
辗转相除法, 又名欧几里德算法,是求最大公约数的一种方法。它的具体做法是:用较大数除以较小数,再用出现的余数(第一余数)去除除数,再用出现的余数(第二余数)去除第一余数,如此反复,直到最后余数是0为止。如果是求两个数的最大公约数,那么最后的除数就是这两个数的最大公约数。
伪代码如下:
◇ 递归法
主调函数:
inputm,n
ifm<n then
t=m, m=n, n=t
endif
gcd(m,n)
outputn
被调函数:
functiongcd(m,n)
r = m mod n
if r = 0 then
output n
else
gcd(n,r)
endif
endfunction
流程图如下:
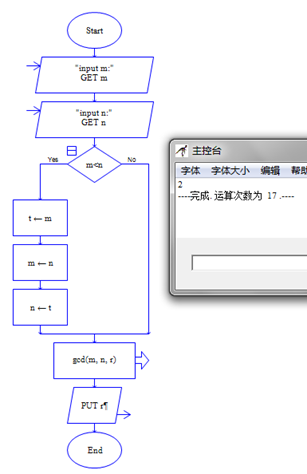
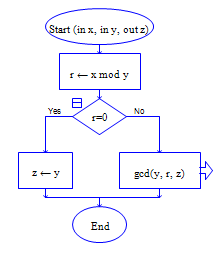
主调函数 被调函数
◇ 非递归
伪代码如下:
inputm,n
ifm<n then
t=m, m=n, n=t
endif
r=mmod n
whiler<>0 do
m=n
n=r
r=m mod n
endwhile
outputn
流程图如下:
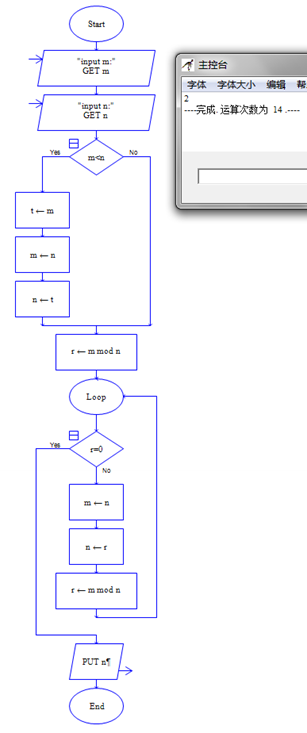
示例2:兔子繁殖问题
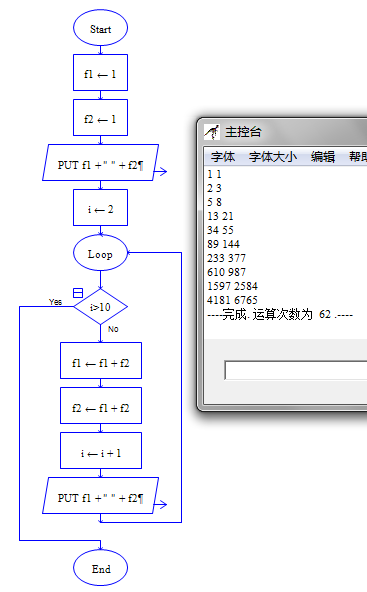
请用迭代法求解斐波那契数列的前20项
解析:
设f1=1,f2=1
f1=f1+f2=2
f2=f1+f2=3
…
伪代码如下:
f1=1
f2=1
outputf1,f2
i=1
whilei<10
f1=f1+f2
f2=f1+f2
output f1,f2
i=i+1
endwhile
流程图如下: