
1、递推算法,常见的算法之一,即通过已知条件,利用特定关系得出中间推论,直至得到结果的算法。和学习一样,由浅入深,由易到难,由简到繁,逐步深化提高。
2、扶贫工作从“输血式扶贫”走向“造血式扶贫”,切断贫困的代际传递。


数列1,3,5,7,9,11,…是一个等差数列;1,3,9,27,81,…是一个等比数列;-1,0,1,0,-1,…是一个摆动数列。这些数列你都可以很容易地写出这些数列的通项公式。
切蛋糕问题。蛋糕切n刀,每一刀都是垂直切,最多可以把这个球形蛋糕切成几块呢?
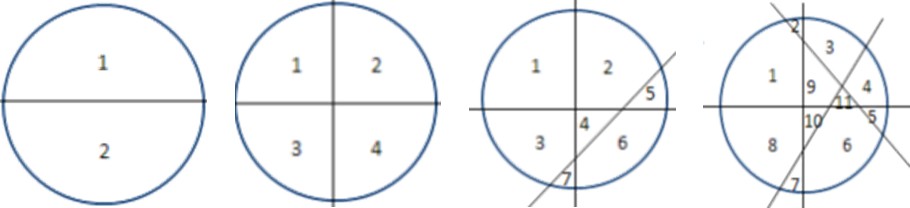
图中可以看出,
切0刀 —— 1块
切1刀 —— 2块
切2刀 —— 4块
切3刀 —— 7块
切4刀 —— 11块
…

你还能写出通项公式吗?直接写出通项比较困难啦。怎么解决呢?
裂项相消法:
1)相邻项之间的关系
ai=ai-1+i(第i刀块数=上一刀块数+本次切的刀数)
2)用迭加法求通项公式
a0=1
a1=a0+1
… …
+) an = an-1 + n
-------------------
an=1+(1+2+…+n)=1+n* (n+1)/2

从问题的规模(项数)出发,找到大规模问题与小规模问题之间的关系(或前后项之间的关联),然后根据他们之间的联系逐步求解。这种在规定的初始条件下,找出后项对前项的依赖关系的操作,称为递推。
表示某项和它前面若干项的关系式就叫递推公式。初始条件称为边界条件。
递推设计
(1)找出递推规律,写出递推公式
(2)根据初始条件,顺推或逆推。
递推实现可以用非递归法实现、也可以用递归法实现。

示例1:兔子繁殖问题
这是一个古典数学问题:有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第3个月后每个月又生一对兔子。假设所有的兔子不死,问第20月兔子总数为多少?
解析:
月数小兔子对数中兔子对数老兔子对数兔子总数
11001
20101
31012
41113
52125
63238
……………
显然这就是著名的斐波那契数列。1,1,2,3,5,8,13,…
(1)找出递推规律,写出递推公式。an=an-1+an-2
(2)根据初始条件,顺推。a1=1,a2=1
伪代码如下:
a[20]=0
a[1]=1, a[2]=1
for i=3 to 20
a[i]=a[i-1]+a[i-2]
endfor
output a[20]
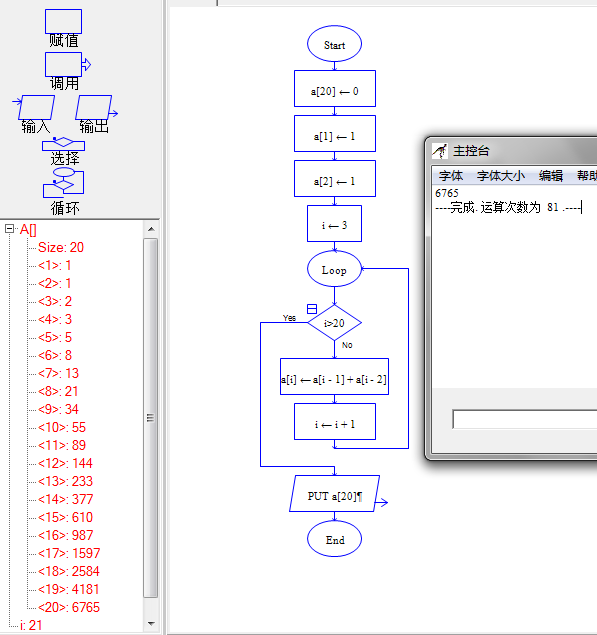
非递归实现
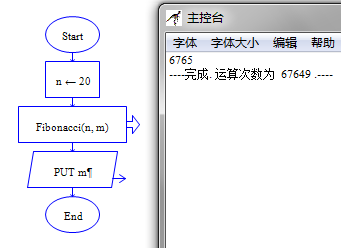
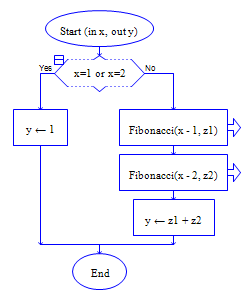
递归实现
示例2:猴子吃桃问题
猴子第一天摘下若干个桃子,当即吃下了一半,还不过瘾,有多吃了一个。第2天早上又将剩下的桃子吃掉了一半,有多吃了一个。以后每天早上都吃了前一天剩下的一半零一个。到第10天早上想再吃时,就只剩下一个桃子了。求第1天共摘了多少个桃子?
解析:
天数 桃子数量
10 1
9 4
8 10
7 22
… ...
1 ?
(1)找出递推规律,写出递推公式。an-1=(an+1)*2。
(2)根据初始条件,顺推或逆推。a10=1。
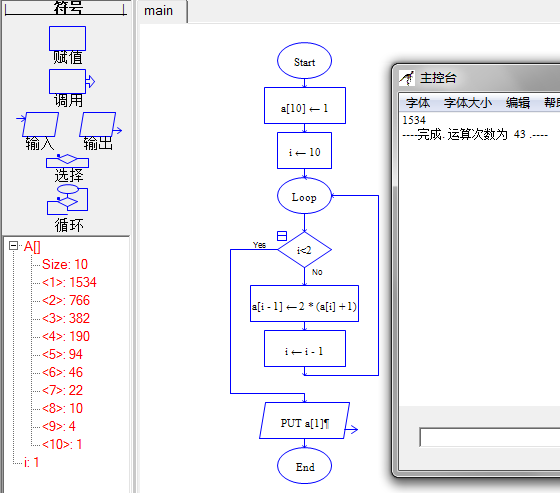
伪代码如下:
a[10]=1
i=10
while i>=2 do
a[i-1]=2*(a[i]+1)
i=i-1
endwhile
output a[1]
非递归式
主调函数:
f=1
monkey(10,f)
output f
被调函数:
function monkey(n,f)
if n>1 then
f=2*(f+1)
monkey(n-1, f)
endif
end function
流程图如下:
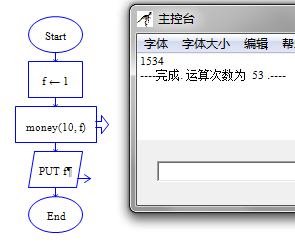
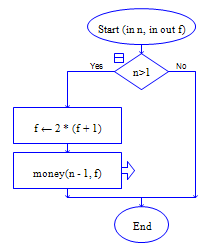
主调函数 被调函数



















