
1、递归算法,常见算法之一,直接或间接调用函数自身,是“自我净化、自我完善、自我革新、自我提高能力”的最佳体现。
2、递归算法——调动自己、脚踏实地。
3、"递归"比喻成"查字典",当你查一个词,发现这个词的解释中某个词仍然不懂,于是你开始查这第二个词。可惜,第二个词里仍然有不懂的词,于是查第三个词,这样查下去,直到有一个词的解释是你完全能看懂的,那么递归走到了尽头,然后你开始后退,逐个明白之前查过的每一个词,最终,你明白了最开始那个词的意思。工匠精神——刨根问底,精益求精,刻苦钻研的体验。

生活中的递归现象很多,比如德罗斯特效应、文字递归和分形图形等。
德罗斯特效应是递归的一种视觉形式,是指一张图片的某个部分与整张图片相同,如此产生无限循环(如下左图);从前有个山,山里有个庙,庙里有个老和尚在给小和尚讲故事,讲的是从前有个山,山里有个庙…,上述文字就是文字递归(如下中图);分形是具有以非整数维形式充填空间的形态特征。通常被定义为“一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状”,即具有自相似的性质(如下右图)。


嵌套函数,就是指在某些情况下,您可能需要将某函数作为另一函数的参数使用,这一函数就是嵌套函数。例如cos(30*pi()/180)),这里cos函数里嵌套了一个pi函数,也就是说pi函数作为cos函数的参数。如果在调用一个函数的过程中又出现直接或间接地调用该函数本身,称为函数的递归调用。如:cos(cos(30*pi()/180))。这里cos函数里直接调用了一个cos函数,被称为递归调用。
递归算法的设计
(1)缩小规模:将原问题转换为性质相似的独立子问题
(2)递归出口:有递归终止的条件
递归算法的三要素
(1)递归式:即递归公式,或递归函数
(2)递归出口:即递归终止条件,类似循环中的初始条件。
(3)界函数:问题规模变化的函数,保证递归规模向出口靠拢,类似循环中的步长。
递归法的实现可以采用条件判断和函数调用。
示例:上述文字递归可以写成如下伪代码
function tell_story()
if ( 讲话被打断 ) then // 递归出口
故事结束;
else
从前有座山;
… …;
tell_story(); // 函数递归调用,递归式
endif
endfunction

示例1:求自然数n的阶乘
一个正整数的阶乘是所有小于及等于该数的正整数的积,并且0的阶乘为1。
解析:阶乘可以用下面两个公式计算。
n! = 1×2×3…×n
n! = n×(n-1)!
如何实现呢?很显然,第一个公式就是循环累乘;而第二个公式就是一个递归公式。
(1)递归式:n×(n-1)!
(2)递归出口:n=0,n=1
(3)界函数:(n-1)!
伪代码如下:
主调函数:
input n
output fact(n)
被调函数:
function fact(n)
if n=1 then
return 1
else
reurn n*fact(n-1)
endif
endfunction
流程图如下:
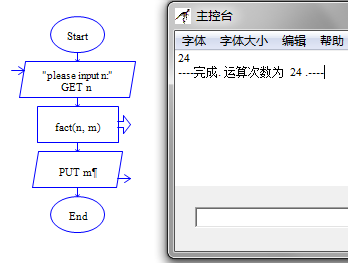
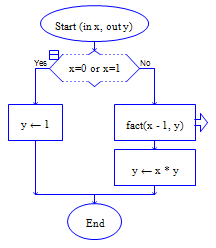
示例2:汉诺塔
古印度有一个梵塔,塔内有3个座A、B、C,开始时A座上有n个盘子,盘子大小不等,大的在下,小的在上。老和尚想把这n个盘子从A座移到C座,但规定每次只允许移动一个盘子,且在移动过程中在3个座上都始终保持大盘在下,小盘在上。移动过程中可以利用B座。请问有m个盘子的汉诺塔全部移动到另外一个柱上时需要移动的最少步数是多少?
解析:假设有n片,移动次数是f(n),显然f(1)=1,f(2)=3,f(3)=7,且f(k+1)=2*f(k)+1。
伪代码如下:
主调函数:
input n
output hanoi(n)
被调函数:
function hanoi(n)
if n=1 then
return 1
else
reurn 2*hanoi(n-1)+1
endif
endfunction
流程图如下:
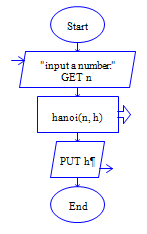
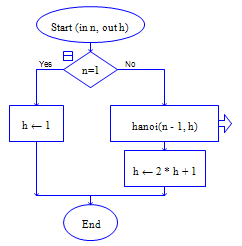
主调函数 被调函数















